Введение в теорию множеств. Операции над множествами. Диаграммы Эйлера–Венна. Законы и тождества алгебры множеств

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

––––––––––––––

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

“МОСКОВСКАЯ ГОСУДАРСТВЕННАЯ АКАДЕМИЯ

ПРИБОРОСТРОЕНИЯ И ИНФОРМАТИКИ”

––––––––––––––––––––––

Кафедра “Персональные компьютеры и сети”

ВВЕДЕНИЕ В ТЕОРИЮ МНОЖЕСТВ

Учебное пособие

(конспект лекций)

Москва

2005

УДК: 519.1(075.8)

ББК 32.973.3

Введение в теорию множеств / В.Н. – М.: МГАПИ, 2005. –  с.

Рекомендовано Ученым Советом МГАПИ в качестве учебного пособия для специальности 2201.

Понятие множества относится к первоначальным понятиям, не подлежащим определению. Считается, что множество задается свойством, обладание которым делает объект принадлежащим этому множеству. При исследовании систем различной физической природы довольно часто они представляются как множества взаимосвязанных или взаимодействующих частей – элементов. Связи между элементами задаются через соответствия или отношения.

Множества, элементы, соответствия, отношения характеризуются определенными свойствами и набором допустимых операций над ними. Об этом и пойдет речь в данном пособии.

Предназначено для студентов, обучающихся по направлению “Информатика и вычислительная техника”. Для специальности 2201 учебное пособие предназначено для использования в курсе “Дискретная математика ”.

Печатается по решению Редакционно–издательского совета Московской государственной академии приборостроения и информатики.

Научный редактор:       д.т.н., проф. Михайлов Б.М.

Рецензенты:                   к.т.н., проф. Рощин А.В., к.т.н., проф. Степанова Т.А.

Работа рассмотрена и одобрена на заседании кафедры ИТ4 “Персональные компьютеры и сети” ____________2005г., протокол № ___.

Ó , 2005

СОДЕРЖАНИЕ

1. МНОЖЕСТВА.. 4

1.1. Основные понятия. 4

1.2. Операции над множествами. 8

1.3. Диаграммы Эйлера–Венна. 12

1.4. Законы и тождества алгебры множеств. 13

1.5. Семейства множеств. 15

1.6. Доказательства. 16

2. СООТВЕТСТВИЯ.. 22

2.1. Соответствия и их свойства. 22

2.2. Функции. 29

2.3. Отображения. 32

2.4. Примеры и упражнения. 34

3. ОТНОШЕНИЯ.. 39

3.1. Бинарные отношения. 40

3.2. Свойства бинарных отношений. 42

3.3. Основные виды отношений. 45

3.4. Операции над бинарными отношениями. 47

3.5. Свойства операций над отношениями. 55

ЛИТЕРАТУРА.. 57

1. МНОЖЕСТВА

Довольно часто состав объекта исследования может быть представлен в виде дискретного множества. Множество – основное понятие в теории множеств, которое вводится без определения. О множестве известно как минимум то, что оно состоит из элементов. Принадлежность элемента множеству оценивается по наличию у него признаков, характеризующих множество.

1.1. Основные понятия

Множество – состоит из элементов. Принадлежность элемента а множеству М обозначается  ("а принадлежит М"), не принадлежность – .

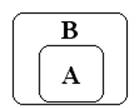
Множество А называется подмножеством множества В (обозначается ), если всякий элемент из А является элементом В (рис 1.1). Если  и , то А называется строгим  подмножеством (обозначается ).

Рисунок 1.1

Содержательные примеры множеств и их возможные обозначения:

М₁ – множество всех операций (работ) по сборке компьютера;

М₂ – множество видов услуг, предоставляемых фирмой "Formoza";

N – множество натуральных чисел 1, 2, 3,...;

N₁ – множество натуральных чисел, не превосходящих 100;

R – множество всех действительных чисел и т.д.

Два определения равенства множеств:

Определение I: Множества А и В равны (А = В), если их элементы совпадают.

Определение II: Множества А и В равны, если  и .

Множество, состоящее из конечного числа элементов, называется конечным, в противном случае – бесконечным (например, множества N, R– бесконечные множества).

Число элементов в конечном множестве М называется его мощностью и обозначается |М|.

Множество мощности 0, т.е. не содержащее элементов, называется пустым (обозначается ): || = 0. Принято считать, что пустое множество является подмножеством любого множества.

В множестве можно задать нижнюю и верхнюю границы, обозначаемые