Для решения систем уравнений методом итераций необходимо чтобы уравнения входящие в их состав были записаны в следующем виде
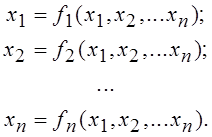 (1)
(1)
Обозначим ![]() -
значение i-го корня
системы полученного на k-ой
итерации. Тогда значение первого корня на k-ой итерации можно записать как:
-
значение i-го корня
системы полученного на k-ой
итерации. Тогда значение первого корня на k-ой итерации можно записать как:
![]() .
(2)
.
(2)
Учитывая, что
найдено значение ![]() , второй корень можно получить двумя
способами:
, второй корень можно получить двумя
способами:
![]() (3)
(3)
или
![]() .
(4)
.
(4)
Значение же n-ого корня можно получить как:
![]() (5)
(5)
или
![]() .
(6)
.
(6)
Очевидно решения (4) и (6) являются предпочтительными, так как используют более точные значения корней уже полученных на текущем шаге. Метод, базирующийся на этой особенности решения, получил название метода Зейделя. В противоположность ему метод, не использующий значения, полученные на текущем шаге, будем называть методом простых итераций.
Анализ показывает, что обычно метод Зейделя дает лучшую сходимость, чем метод простых итераций т.е. для получения результата требуется меньшее число шагов и как следствие минимизируется время счета. Иногда процесс Зейделя может сходиться даже в том случае, если расходится процесс итерации. Однако это бывает не всегда. Возможны случаи, когда процесс Зейделя сходится медленнее процесса итераций.
Приведение системы уравнений к итерационному виду.
Пусть дана следующая система уравнений:
4*X1 + 0.24*X2 - 0.08*X3 = 8,
0.09*X1 + 3*X2 - 0.15*X3 = 9,
0.04*X1 - 0.08*X2 + 4*X3 = 20.
Выразим X1 из первого уравнения, X2 из второго и X3 из третьего. Тогда получаем нашу систему уравнений в виде удобном для решения методом итераций:
X1 = -0.06*X2 + 0.02*X3 + 2,
X2 = -0.03*X1 + 0.05*X2 +3,
X3 = -0.01*X1 + 0.02*X2 + 5.
Порядок проведения работы
1. Записать систему уравнений в итерационном виде.
2. Запустить программу Lab4.exe и выполнить задание.
Задание
1.
Для
указанных в варианте значений,
методом простых итераций и методом Зейделя, с
точностью ![]() решить
систему уравнений:
решить
систему уравнений:
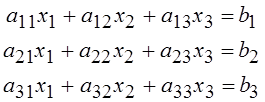
2.
Провести
решение с точностью ![]() ,
, ![]() ,
,![]() ...
... ![]() и
построить графики зависимостей числа требуемых итераций от заданной точности
решения для обоих методов.
и
построить графики зависимостей числа требуемых итераций от заданной точности
решения для обоих методов.
3.
Построить
графики изменения значения любого из корней для итераций с первой по десятой у
каждого из методов (при точности ![]() ).
).
Результаты работы
По окончанию работы необходимо иметьь:
1. Систему уравнений преобразованную в вид удобный для итераций
2. Решение (корни системы уравнений)
3. Полученные графики
Варианты
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.