Нахождение математического ожидания и дисперсии случайной величины. Вычисление объема / площади фигур методом Монте Карло, страница 2

Курс «Численные методы».

Лабораторная работа №3

Интерполирование функций

Для выполнения данной лабораторной работы необходимо запустить исполняемый файл lab3.exe. Далее следует выбрать функцию указанную  в Вашем варианте (рис 1.).

Рисунок 1. Интерфейс программы.

Необходимо определить зависимость относительной погрешности интерполированного значения функции от:

n количества узлов интерполирования,

n размера отрезка интерполирования.

Для получения зависимости погрешности от количества узлов интерполирования необходимо установить границы отрезка интерполирования равными a и в (из варианта). Теперь изменяя число узлов интерполирования от 2 до 20 с шагом 2 необходимо получить интерполированное значение функции в заданной точке x и его относительную погрешность (табл. 1). По таблице построить график зависимости. Вычисления производить с точностью 6 дробных знаков.

Таблица 1.

Для получения зависимости погрешности от длины отрезка интерполирования необходимо провести 10 (i=1..10) вычислений в каждом из которых изменять значения a и в по следующему правилу:

;                , где , ,

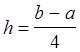Число узлов интерполяции взять равным  n (см. вар).

Результаты вычислений завести в таблицу и построить график зависимости.

Таблица 2.