Одноразрядные двоичные сумматоры. Карты Карно для переноса и суммы. Схема одноразрядного сумматора, реализующая уравнения

4. СУММАТОРЫ

4.1. Одноразрядные двоичные сумматоры

Процесс суммирования одноразрядных двоичных чисел описывается таблицей истинности (табл. 4.1)

Таблица 4.1

В этой таблице X_i, Y_i – произвольные разряды слагаемых, P_i–1 – перенос из предыдущего разряда, P_i – перенос в следующий разряд, S_i – разряд суммы.

Карты Карно для переноса и суммы дают следующие дизъюнктивные нормальные формы

P_i

S_i

                                                 

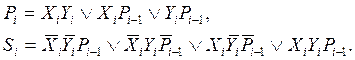
На рис. 4.1 показана схема одноразрядного сумматора, реализующая  уравнения (1), (2).

Как видим, у схемы имеются два существенных недостатка:

- функция суммы реализуется достаточно сложно, поскольку не поддается минимизации;

- требуются как прямые, так и инверсные значения разрядов слагаемых.

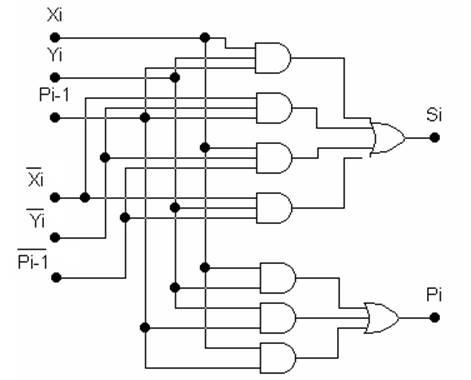
Рис. 4.1 Схема одноразрядного сумматора,

реализующая выражения (1), (2)

Логическое выражение для суммы, в котором отсутствуют инверсные значения слагаемых и входного переноса, может быть получено при рассмотрении суммы как функции четырех переменных  X_i, Y_i, P_i–1, P_i, где P_i – перенос, образующийся в результате сложения X_i, Y_i, P_i–1.

Таблица истинности функции S_i = f(X_i, Y_i, P_i–1, P_i) приведена в табл. 4.2.

Таблица 4.2                                                 

Xi	Yi	Pi-1	Pi	Si
0	0	0	0	0
0	0	0	1	*
0	0	1	0	1
0	0	1	1	*
0	1	0	0	1
0	1	0	1	*
0	1	1	0	*
0	1	1	1	0
1	0	0	0	1
1	0	0	1	*
1	0	1	0	*
1	0	1	1	0
1	1	0	0	*
1	1	0	1	0
1	1	1	0	*
1	1	1	1	1

В колонке S_i  проставлены символы * в случаях, когда в колонке выходного переноса P_i  появляются значения 1 или 0, которые не могут получиться при сложении входных переменных X_i, Y_i и P_i–1. Такое представление позволяет рассматривать сумму S_i  как частично определенную функцию.

Для минимизации S_i составим карту Карно

 ,                                                                               (3)

                (4)

Схема одноразрядного сумматора, реализующая выражения (3) и (4), показана на рис. 4.2.

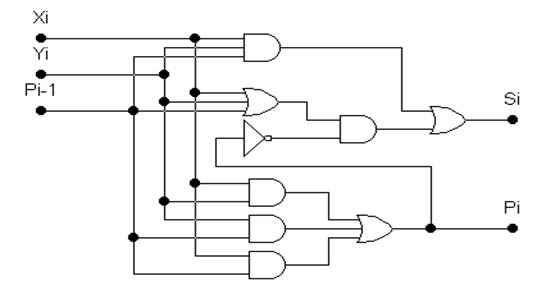Рис. 4.2 Схема сумматора, реализующая выражения (3) и (4).

При построении сумматоров с использованием готовых элементов М2 (“сумма по модулю 2”) уравнения для P_i и S_i могут быть представлены в следующем виде: