Одноразрядные двоичные сумматоры. Карты Карно для переноса и суммы. Схема одноразрядного сумматора, реализующая уравнения, страница 2

                                                               (5)

                                                                       (6)

Задание 1. Покажите самостоятельно, что выражения (5) и (6) соответствуют приведенной выше таблице истинности, показанной в табл. 4.1.

Такое представление позволяет реализовать одноразрядный сумматор схемой, показанной на рис. 4.3.

Рис. 4.3. Сумматор из готовых элементов М2,

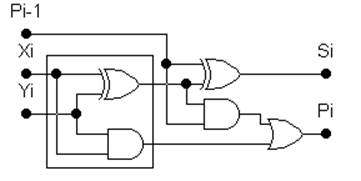реализующий выражения (5) и (6).

Выделенную часть схемы называют полусумматором и обозначают в Electronics Workbench так, как показано на рис. 4.4,а. На этом же рисунке показано обозначение полного одноразрядного сумматора (б).

На рис. 4.4 обозначено: A и B – слагаемые; Ci, Co – входной и выходной перенос, соответственно;  – выход суммы (для полусумматора зависит только от A и B).

Рис. 4.4. Обозначение схем в Electronic Workbench:

а – полусумматор; б – полный сумматор

ЗАДАНИЕ 2. Для схемы, показанной на рис. 4.5, запишите выражения выходов D и E, как функций входов A, B, C.

Рис. 4.5. Схема к заданию 2

4.2. Двоичный сумматор с последовательным переносом

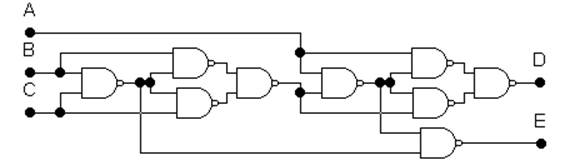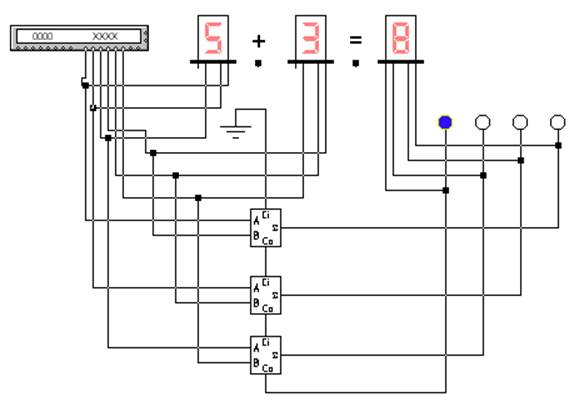
Многоразрядные (n-разрядные) сумматоры создаются на базе одного полусумматора и n–1 полных сумматоров (или n полных сумматоров – в этом случае присутствует вход переноса младшего разряда). На рис. 4.6 в качестве примера показана схема простейшего трехразрядного сумматора с последовательным переносом. На вход C_i первого разряда подан низкий уровень напряжения (логический 0).

4.3. Двоичный сумматор с групповым переносом

Недостаток многоразрядных двоичных сумматоров с последовательным переносом – большое время выполнения операции суммирования, равное сумме времени распространения переносов плюс время получения суммы в последнем разряде. В этих сумматорах приходится принимать суммарное время распространения переносов равным максимальному значению n, где n – число разрядов в сумматоре,  – время формирования переноса в одном разряде, в то время как на практике средняя длина цепочки переносов равна  разрядов.

С целью сокращения времени распространения переносов создают сумматоры с параллельным переносом, т. е. схему, в которой перенос во всех разрядах формируется одновременно.

Ранее для сигнала переноса из i-го разряда было получено выражение

Представим его в таком виде

.                                                          (7)

Функцию

G_i = X_iY_i

называют функцией генерации переносов, а функцию

D_i =

– функцией прозрачности.

Функции G_i и D_i формируются обычно отдельными элементами И и ИЛИ.

Рис. 4.6. Трехразрядный сумматор с последовательным переносом

Используя формулу (7) для переносов Р_i-1, P_i-2, … P₁, для переноса из i–го разряда получим

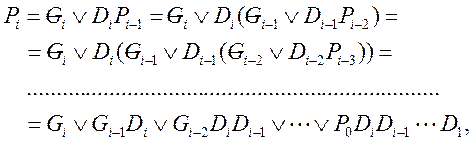                                   (8)

где P₀ – перенос в самый младший первый разряд.

Из последнего выражения можно получить формулы для переноса из любого разряда, подставляя значение i и исключая все члены с неположительными и нулевыми индексами (кроме Р₀).

Например, для переносов из четырехразрядной группы, не являющейся первой, получаем

 

,

.

Для первой группы, у которой нет входного переноса P₀, будем иметь

      

,

.

Поскольку значения G_i и D_i в каждом разряде не зависят от переносов из младших разрядов, а зависят только от значений слагаемых в этом разряде, то возможно формирование переноса P_i  на основе анализа значений разрядов всех слагаемых и переноса P₀ в самый младший разряд. Сформированный таким образом сигнал называют сигналом параллельного переноса. Время формирования этого сигнала будет равно времени срабатывания элементов И–ИЛИ. Однако для формирования сигнала P_i эти элементы должны иметь не менее i+1 входов, выходы формирователей сигналов D_i будут нагружены на большое число элементов, поэтому аппаратные затраты на реализацию параллельного переноса оказываются значительными. Кроме того, поскольку в сериях интегральных схем существует ограничение на число входов элементов, для реализации параллельного переноса приходится создавать многоярусные схемы И и ИЛИ, что снижает его эффективность.