Одноразрядные двоичные сумматоры. Карты Карно для переноса и суммы. Схема одноразрядного сумматора, реализующая уравнения, страница 3

Используя метод разбиения разрядов сумматора на группы, можно построить схемы параллельного переноса внутри групп, а затем, применив аналогичный подход, можно создать схему параллельного переноса между группами. Такой способ позволяет получить значительный выигрыш по быстродействию за счет дополнительных аппаратурных затрат.

Некоторое снижение объема оборудования получается при разбиении сумматора на группы разной длины. Однако при этом получается нерегулярная структура сумматора. Поэтому чаще всего рекомендуется разбиение сумматоров на группы с одинаковым числом разрядов (до 8).

ЗАДАНИЕ 3. Разработайте четырехразрядную группу сумматора с параллельным переносом.

4.4. Двоичный сумматор–вычитатель

Суммирование здесь выполняется как в обычном двоичном сумматоре, а вычитание заменяется сложением в дополнительном коде.

Напомним, дополнительный код положительного двоичного числа совпадает с его прямым кодом. Дополнительный код отрицательного числа образуется из обратного кода добавлением 1 в младший разряд.

При кодировании двоичных чисел самый старший разряд отводится под знак числа: 0 – число положительное, 1 – число отрицательное.

Пример.

Положительное число + 6 в двоичной системе счисления с учетом знака числа имеет код (как прямой, так и дополнительный) 0 110 (знаковый разряд отделен пробелом).

Отрицательное число – 6 имеет прямой код 1 110, обратный код 1 001 и дополнительный код 1 010.

Поскольку суммирование положительных чисел это просто сложение прямых кодов, а вычитание – сложение дополнительных кодов, то для реализации двоичного сумматора–вычитателя нужен двоичный сумматор и преобразователи отрицательных чисел в дополнительный код. Получить обратный код отрицательного числа можно с помощью элементов М2, работающих в режиме управляемого инвертора (см. рис. 4.7), а добавить к обратному коду 1 можно с помощью сумматора, необходимого для выполнения основной операции – суммирования.

	U	X	Y
0	0	0	0	U = 0 Y = X
1	0	1	1
2	1	0	1	U = 1 Y =
3	1	1	0

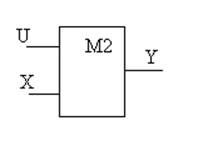
Рис. 4.7. Управляемый инвертор

Схема четырехразрядного сумматора–вычитателя показана на рис. 4.8, где слагаемое А подается с генератора двоичных слов, слагаемое В фиксировано и равно 3. Результат С получается таким .

Переключение сложение – вычитание осуществляется переключателем Space.

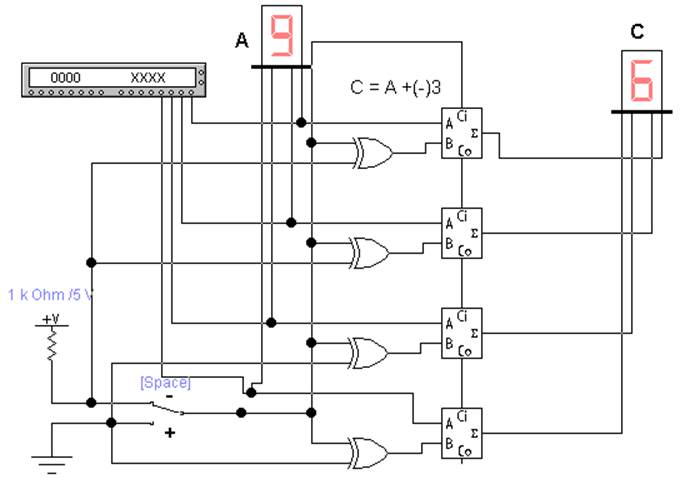
Рис. 4.8. Трехразрядный двоичный сумматор–вычитатель

4.5. Четырехразрядное АЛУ

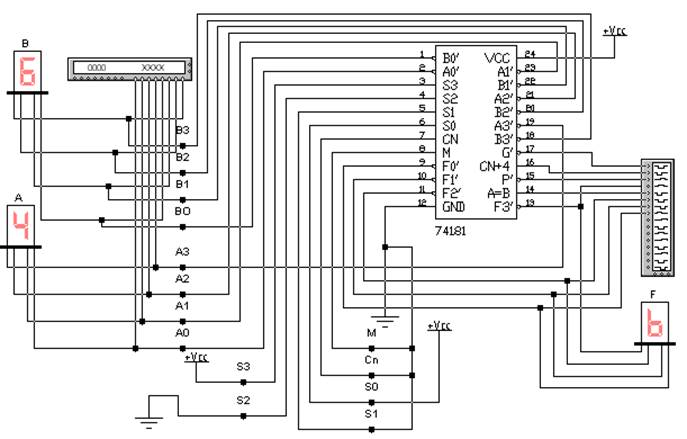
В базе данных Electronics Workbench имеется микросхема 74181 четырехразрядного арифметико-логического устройства (АЛУ) (отечественный аналог К155ИП3). Данное АЛУ может работать в 32 режимах в зависимости от управляющих сигналов на входах M, S3, S2, S1, S0. В библиотеке программы Electronics Workbench приведена схема включения этого АЛУ в режиме сумматора с переносом из младшей тетрады (рис. 4.9). В рассмотренном случае вычисления выполняются по формуле

F = A + B +1.

Все возможные режимы работы микросхемы К155ИП3 подробно изложены в [1], а ее функциональная схема дана, например, в [2].

Рис. 4.9. Схема включения четырехразрядного АЛУ (микросхема 74181)

4.6. Одноразрядный двоично‑десятичный сумматор

Сумма двух одноразрядных десятичных чисел с учетом переноса из младшей декады может принимать значения 0…19 (19, т.к. 9+9= 18+ 1 переноса).

Все возможные варианты суммы двух одноразрядных десятичных чисел показаны в табл. 4.3.

В таблице символом * обозначен перенос, которого нет, но он должен быть, так как сумма  10.

Вычитание 10 можно заменить сложением с дополнительным кодом 10.

10 в двоичной системе – это  1010.

Обратный код  10 – это 0101.

Дополнительный код 10 получается таким 0101 + 0001 = 0110 (в десятичной системе это 6).

Таким образом, коррекция суммы от 10 до 19 сводится к добавлению 6. Признаком необходимости такой коррекции является наличие переноса. Правда, перенос получается автоматически только для сумм 16…19, а для сумм 10…15 его необходимо создать.