Математика \ Дискретная математика

Одноразрядные двоичные сумматоры. Карты Карно для переноса и суммы. Схема одноразрядного сумматора, реализующая уравнения, страница 5

Таблица 4.4                                                             

84\21

00

01

11

10

00

01

11

1*

1*

1*

1*

10

1*

1*

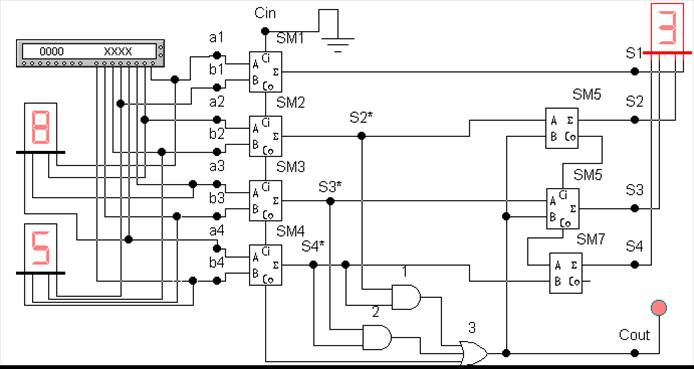
Схема двоично-десятичного сумматора состоит из трех частей:

-  SM1, SM2, SM3, SM4 – выполняют первый этап сложения и формирование промежуточной суммы;

-  SM5, SM6, SM7 – выполняют коррекцию промежуточной суммы, т.е. сложение с числом +6 (0110 в двоичном коде), и формирование окончательного результата суммы на выходах S1, S2, S3, S4 (при этом S1 передается из SM1 без изменения);

-  элементы И1, И2, и ИЛИ3 (на рис. 4.10) образуют схему выработки корректирующей поправки +6 и формирования сигнала десятичного переноса Cout в следующую тетраду.

Для того чтобы убедиться в правильности работы схемы рис. 4.10, достаточно рассмотреть три возможных случая:

1)  A + B < 10. Коррекция не требуется (поправка равна 0), а перенос Cout не возникает.

2)  10 ≤ A + B ≤ 15. Тогда перенос Co из SM4 не возникает, но сигнал коррекции на выходе элемента ИЛИ3 равен 1, ибо в указанном диапазоне суммы имеем . Этот сигнал коррекции используется как поправка +6 в SM5, SM6, SM7 и как сигнал переноса Cout.

3)  16 ≤ A + B ≤ 19 с учетом возможного переноса Cin из младшей тетрады. В этом случае из SM4 автоматически возникает сигнал переноса Co, который используется как поправка +6 и как сигнал Cout. Заметим, что на SM1 … SM4 получается промежуточная сумма      0 ≤ (A + B)п ≤ 3, а после коррекции на SM5 … SM7 — окончательная сумма    6 ≤ (A + B) ≤ 9.


Рис. 4.10. Двоично-десятичный сумматор

ЗАДАНИЕ 4. Проверьте правильность работы тетрады двоично-десятичного сумматора подачей слагаемых A и B, таких, чтобы A + B < 10; 10 ≤ A + B < 16;  A + B > 16.

Известен другой способ суммирования положительных десятичных чисел, не требующий проведения коррекции результата, полученного на выходе четырехразрядного сумматора. Для его обоснования воспользуемся табл. 4.5.

В первой графе n табл. 4.5 представлены в десятичной системе счисления все числа, которые могут быть получены на выходе четырехразрядного сумматора при сложении одноразрядных десятичных чисел от 0 до 9 с учетом входного переноса с0 = 1. Максимальное число равно 9 + 9 + 1=19. В последующих пяти графах эти же числа записаны в виде 5-разрядных двоичных чисел, которые могут быть получены как выходные сигналы переноса с1и суммы s3, s2, s1, s0 четырехразрядного двоичного сумматора. В правой части табл. 4.4 десятичные числа от 0 до 19 записаны в том виде, который они должны иметь на выходе одноразрядного десятичного сумматора, а именно в виде сигнала переноса С1 и кода 8-4-2-1 (S3 S2 S1 S0). Отметим, что перенос С1 отражает значения старшего разряда, а код S3 S2 S1 S0 – значения младшего разряда двухразрядного десятичного числа. Для схемной реализации одноразрядного десятичного сумматора необходимо синтезировать комбинационную схему, преобразующую приведенные в табл. 4.4 выходные сигналы двоичного сумматора с1, s3, s2, s1, s0 в требуемые сигналы С1, S3, S2, S1, S0.Из табл. 4.4 видно, что s0 = S0. Поэтому задача синтеза упрощается: необходимо построить комбинационную схему на 4 входа (с1, s3, s2, s1) и 4 выхода, (С1, S3, S2, S1,), используя при этом 9 наборов входных переменных, так как при n, равном 0 и 1, 2 и 3, 4 и 5 и т. д., одноименные входные переменные имеют одинаковые значения.

                                                             Таблица 4.5

Скачать файл