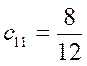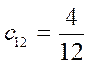Cистема национальных счетов – инструмент макроэкономического анализа. Система индексов в аналитическом изучении динамики материальных и финансовых потоков, страница 27

,     и т. д.

В результате матрица С' приобретает следующий вид:

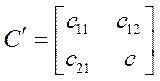
Транспортирование матрицы С' дает матрицу С, равную

.

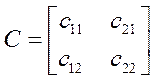Элементы матрицы С характеризуют внутриотраслевую товарную структуру (технологию) валового выпуска.

Диагональная матрица gформируется в соответствии с методологией, описанной в методических рекомендациях к решению типовой задачи 6.11.

Матрица С через диагональную матрицу находится в опосредованной взаимосвязи с транспонированной матрицей V', т. е.

.

В соблюдении этого тождества рекомендуется убедиться на основе данных условия задачи 6.15. Выполнение этого условия свидетельствует о правильности найденных коэффициентов внутриотраслевой товарной структуры (технологии) валового выпуска.

Методические указания к решению типовой задачи 6.17

В условии задачи дана матрица С, равная

.

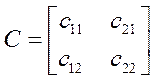Необходимо найти обратную ей матрицу С^-1. Обращение матрицы С производится в соответствии со следующей формулой:

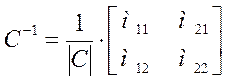, где |С| – детерминант матрицы С, равный с₁₁ · с₂₂— с₁₂ · с₂₁; м₁₁, м₂₁, м₁₂, м₂₂ – алгебраические дополнения соответствующих элементов матрицы С.

Алгебраические дополнения находятся по следующим формулам:

;

;

;

.

После нахождения определителя |С| и алгебраических дополнений остается только подставить их значения в формулу обратной матрицы С^-1 и перемножить.

Обратная матрица С^-1 используется для нахождения симметричной матрицы А типа товар х товар (см. рекомендации к решению задачи 6.19).

Методические указания к решению типовой задачи 6.19

Матрица А находится на основе матриц В и С^-1 по формуле

.

Значения матриц В и С^{-1 см. в решениях типовых задач 6.11 и 6.17. Матрица А является симметричной (квадратной) типа товар х товар. Элементы матрицы А являются коэффициентами прямых затрат (потребления)} i-го товара на производство j-го товара.

Методические указания к решению типовой задачи 6.21

Решение задачи 6.21 осуществляется в два этапа. На первом этапе находится матрица (1 — А) как разность между единичной матрицей и матрицей А, т. е.

.

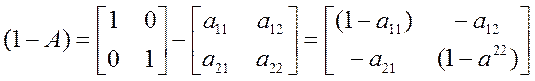На втором этапе производится обращение матрицы (1 — А) в соответствии с методологией, описанной в методических рекомендациях к решению типовой задачи 6.19, однако применительно к данным условия задачи 6.21.

Обратная матрица (1 — А)^-1 известна как матрица Леонтьева. Она характеризует полные затраты товаров на производство конечного продукта и используется в анализе взаимосвязи валового выпуска в зависимости от конечного спроса (см. рекомендации к решению типовой задачи 6.23).

Методические указания к решению типовой задачи 6.2

Для анализа взаимосвязи валового выпуска с конечным спросом разрабатывается следующее уравнение:

,

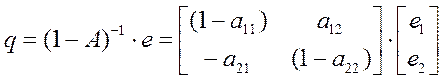где е – конечный спрос; q – валовой выпуск.

Рекомендуется подставить данные условия задачи в выше приведенное уравнение и произвести умножение матрицы (1 — А)^-1 на вектор-столбец е.

Во второй части решения задачи задается приращение конечного спроса. Последующая его подстановка в формулу после несложных матричных вычислений покажет ожидаемое приращение валового выпуска. Для определения эластичности необходимо абсолютные значения прироста функции превратить в относительные, показав, на сколько процентов увеличится валовой выпуск при росте конечного спроса на один процент.

ОГЛАВЛЕНИЕ

В в е д е н и е

1.  Система национальных счетов – инструмент макроэкономического анализа                                  

2. Система индексов в аналитическом изучении динамики материальных и финансовых ресурсов    

3. Методы переоценки ВВП и его компонентов в постоянные цены   

4. Переоценка в постоянные цены активов экономики     

5 Многофакторный  индексный  анализ  макроэкономических показателей                                                                    

6. Моделирование и анализ интегральных показателей эффективности потребленных и примененных ресурсов                                            

7. Учебно-методическое обеспечение практических занятий