Cистема национальных счетов – инструмент макроэкономического анализа. Система индексов в аналитическом изучении динамики материальных и финансовых потоков, страница 26

Конечный спрос на товары определяется по данным матрицы использования товаров и услуг в соответствии с формулами задачи 6.1., с помощью которых находятся показатели е₁ и е₂.

При наличии данных о валовом выпуске и промежуточном потреблении в отраслях показатели валовой добавленной стоимости по производственному методу могут быть исчислены в соответствии с формулами задачи 6.1, определяющими значения показателей у₁и у₂. Полученные результаты заносятся в клеточки с условными обозначениями у₁' и у₂'. После проверки взаимной сбалансированности итоговых показателей (η должно быть равно η') решение задачи завершается.

Методические указания к решению типовой задачи 6.11

Матрица В коэффициентов затрат типа товар х отрасль разрабатывается на основе данных U-матрицы. Ее элементы bij определяются по формуле

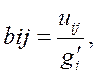
где i– номер строки (товара); j– номер столбца (отрасли).

Исходя из условных обозначений табл. 6.1, элемент b₁₁ матрицы В в соответствии с ранее приведенной формулой будет равен частному отделения элемента и₁₁ матрицы Uна итоговое значение затрат g₁', т. е.

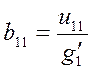
и соответственно

;   ;   .

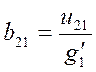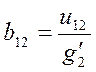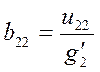Диагональная матрица  соsстоит из элементов g₁' и g₂', тождественных по своему численному значению g₂и g₁, расположенных по диагонали слева вниз направо, т. е.

.

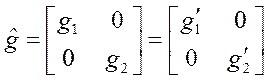Следует напомнить при этом, что диагональные значения матрицы характеризуют валовой выпуск в отраслях экономики. Что касается коэффициентов b_ij, то они предназначаются для характеристики прямых затрат (промежуточного потребления) товаров в расчете на единицу валового выпуска в отраслях.

Матрицы U, В и взаимосвязаны между собой так, что произведение матрицы В на диагональную матрицу , т. е. дает матрицу U.

.

При решении задачи в этом следует убедиться на примере числовых данных задач 6.11 и 6.12. Вышеприведенная взаимосвязь трех матриц позволяет проверить правильность исчисления коэффициентов прямых затрат в расчете на единицу валового выпуска в отраслях. При стабильных коэффициентах затрат (неизменней отраслевой технологии производства товаров данное тождество показывает, что промежуточное потребление в отраслях пропорционально валовому выпуску.

Коэффициенты матрицы В используются для преобразования матрицы Uв матрицу коэффициентов прямых затрат типа товар х товар, характеризующих удельное потребление товара iна производство товара j.

Методические указания к решению типовой задачи 6.13

Матрицы U и Vприводятся в условии задачи: первая — на пересечении 1-й и 2-й строк с третьим и четвертым столбцами; вторая — на пересечении 3-й и 4-й строк с 1-м и 2-м столбцами.

Элементы матрицы Dисчисляются по данным F-матрицы в соответствии с формулой

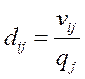
Например, по данным условия задачи 6.13

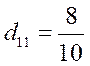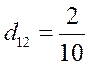;     и т. д.

Диагональная матрица состоит из элементов q₁' и q₂', тождественных по своему численному значению q₁и q₂, которые располагаются по диагонали слева вниз направо, т. е.

.

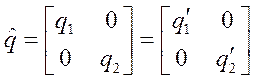При этом следует заметить, что диагональные значения матрицы характеризуют валовой выпуск отдельных видов (групп) товаров. Коэффициенты d_ijпоказывают удельный вес отраслей (товарную межотраслевую структуру) в общем объеме производства каждого из товаров.

Матрицы D, , и Vвзаимосвязаны между собой. Эта взаимосвязь описывается тождеством

, в справедливости которого предлагается убедиться на основе данных условия задачи. Тождество показывает, что в условиях стабильной межотраслевой структуры производства товаров объем производства каждого товара пропорционален совокупному их валовому выпуску.

Методические указания к решению типовой задачи 6.15

В аналитических преобразованиях матриц типа товар х отрасль и отрасль х товар в симметричную матрицу типа товар х товар используется матрица С. Матрица С – транспортированная С' – матрица, отдельные элементы которой находятся в соответствии с формулой

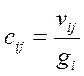
где v_ij– элементы матрицы Vпри i-м номере строки (отрасли), j-м номере столбца (товара); g_i— валовой выпуск i-й отрасли.

Например, по данным условия задачи 6.15 будем иметь