Коэффициент усиления системы определяется по формуле:
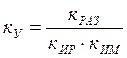 ,
(19)
,
(19)
где кир – коэффициент передачи измерителя рассогласования, ким – коэффициент передачи исполнительного механизма.
Для измерителя рассогласования, реализованного на потенциометрах по каскадной схеме, коэффициент определяется следующим образом:
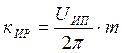 ,
(20)
,
(20)
где m – число точек связи между датчиком и приемником.
В данном случае m=4.
Коэффициент передачи исполнительного механизма определяется по формуле:
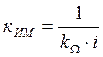 ,
(21)
,
(21)
где кΩ – коэффициент пропорциональности между напряжением и скоростью, определяется по формуле:
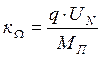 (22)
(22)
6.2 Статический расчет.
По формуле (18) рассчитаем жесткость механической характеристики:
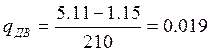 Н·м·с
Н·м·с
По формуле (17) рассчитаем коэффициент передачи разомкнутой системы:
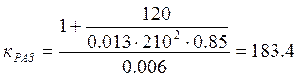 с-1
с-1
По формуле (20) определим коэффициент передачи измерителя рассогласования:
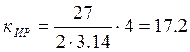 В
В
Коэффициент пропорциональности напряжения и скорости рассчитаем по формуле (22):
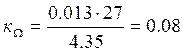 В·с
В·с
Коэффициент передачи исполнительного механизма определим по формуле (21):
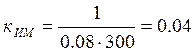 В-1·с-1
В-1·с-1
Коэффициент усиления системы определим по формуле (19):
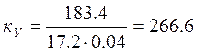
7.1 Расчетная схема и формулы.
Динамический расчет служит для анализа динамических свойств системы, построенной на заданных элементах.
Расчетная схема исполнительного механизма представлена на рис.10.
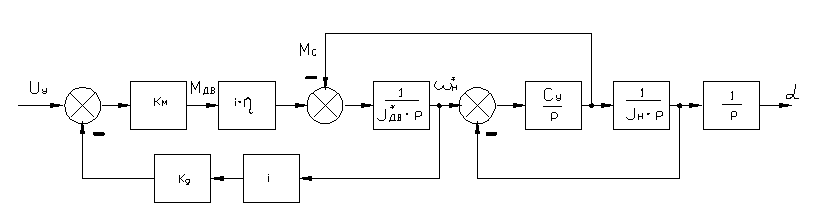
Рис.10.Расчетная схема исполнительного механизма..
Данную расчетную схему можно использовать только в случае кусочно-линейной аппроксимации.
На схеме приняты следующие обозначения:
UУ – напряжение с выхода усилительно-преобразовательного устройства;
α – угол поворота объекта управления;
км – коэффициент пропорциональности между напряжением и моментом, рассчитывается по формуле:
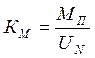 ; (23)
; (23)
кΩ – коэффициент пропорциональности между напряжением и скоростью, рассчитывается по формуле:
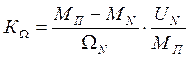 ; (24)
; (24)
МС – момент сопротивления движения;
JДВ* - момент инерции исполнительного двигателя и передаточного механизма, приведенный к выходному валу, рассчитывается по формуле:
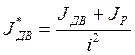 ; (25)
; (25)
ωн* - скорость вращения нагрузки, приведенная к выходному валу;
CУ – коэффициент упругого скручивания, примем значение коэффициента CУ=100 Н·м/рад
p – оператор Лапласа, p=jω.
Данной расчетной схеме соответствует следующая передаточная функция:
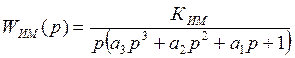 , (26)
, (26)
где
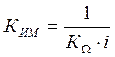 (27)
(27)
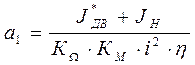 (28)
(28)
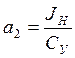 (29)
(29)
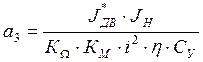 (30)
(30)
7.2. Динамический расчет.
По формуле (23) рассчитаем коэффициент пропорциональности между напряжением и моментом:
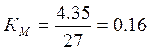 Н·м/В
Н·м/В
По формуле (24) рассчитаем коэффициент пропорциональности между напряжением и скоростью:
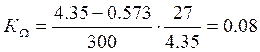 В
В
По формуле (25) рассчитаем приведенный момент инерции:
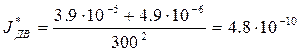 кг·м2
кг·м2
По формулам (27), (28), (29), (30) рассчитаем значения коэффициентов передаточной функции:
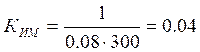
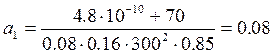
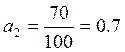
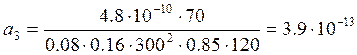
Таким образом, передаточная функция имеет следующий вид:
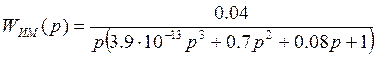
Для проверки устойчивости системы на ее вход подается единичный скачок и оценивается переходный процесс.
Расчетная схема привода антенн представлена на рис.11.
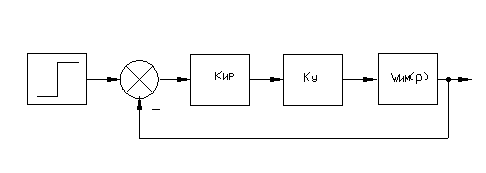
Рис.11. Расчетная схема привода антенн.
Из статического расчета:
![]() В
В
![]()
Переходный процесс рассматриваемой системы представлен на рис.12.
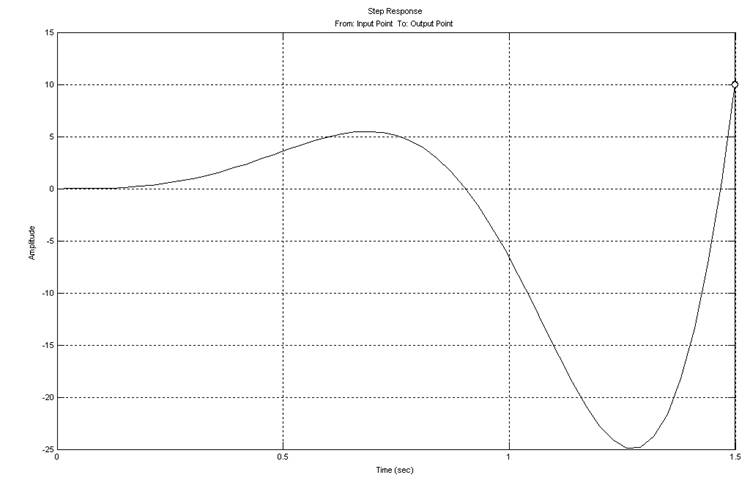
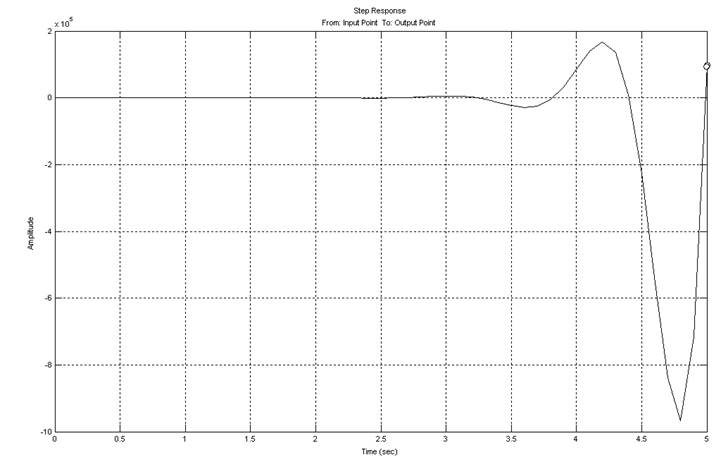
Рис.12. График переходного процесса
Как видно из графика, переходный процесс является расходящимся.
Управление системой в таком режиме невозможно.
Следовательно, необходима коррекция ее динамических свойств.
8.1. Расчетные формулы.
Требуется построить располагаемую амплитудную логарифмическую характеристику (ЛАХ).
Для этого представим передаточную функцию системы в следующем виде:
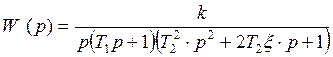 , где К=КИР ·
КУ · КИМ=17.2 · 266.6 · 0.04=183.4
, где К=КИР ·
КУ · КИМ=17.2 · 266.6 · 0.04=183.4
Т1, Т2, ξ – находятся из решения кубического уравнения, стоящего в знаменателе передаточной функции.
Т1=2·1011,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.