Проектирование электропривода антенн. Выбор исполнительного двигателя. Расчет основных параметров редуктора, страница 2

2.3 Характеристики двигателя.

Ми-II исполнительный двигатели для систем автоматики, выполняемые с параллельным или независимым возбуждением. И в этом и в другом случае могут выполняться с тахогенератором  или без него. Управление двигателем осуществляется с помощью изменения напряжения якорной цепи.

.

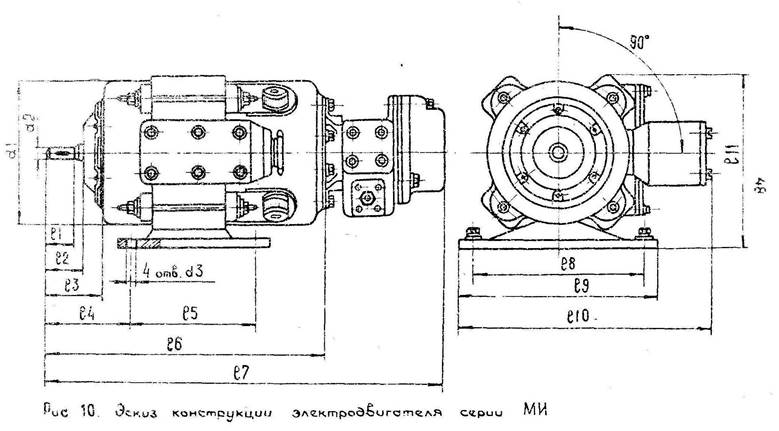
Рис.1.скиз конструкции электродвигателя серии МИ-22

Технические данные двигателя представлены в табл.1, его размеры – в табл. 2.

Таблица 1. Характеристики двигателя МИ-22

Таблица 2. Габаритные и установочные размеры

Размеры, мм
D1	d2	d3	L1	L2	L3	L4	L5	L6	L7	L8	L9	L10	L11
164	16	8	34	42	59	96	128	308	445	216	246	330	180

3. Расчет основных параметров редуктора.

3.1 Расчет оптимального передаточного числа редуктора.

По формуле (3) был рассчитан коэффициент передачи редуктора.

Это значение может оказаться неоптимальным с точки зрения быстродействия системы.

К тому же в этом коэффициенте передачи редуктора учтена только угловая скорость и не учтено угловое ускорение.

Требуется найти оптимальное передаточное число, обеспечивающее минимум пускового момента и максимальное угловое ускорение.

Увеличение углового ускорения двигателя улучшает энергетические характеристики системы, поскольку уменьшается потребляемая мощность и форсирование двигателя по моменту.

Однако оптимальное передаточное число не должно превышать выбранное ранее, чтобы не увеличивать массогабаритные показатели редуктора и его инерционность.

Приравняем эквивалентный и номинальный моменты.

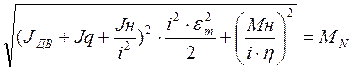
Из этого соотношения, решив квадратное уравнение относительно i, найдем максимальное и минимальное значение передаточного числа:

i_min=90

i_max=1000

Графики эквивалентного Me(i)   и номинального Mn  моментов приведены на рис.2.

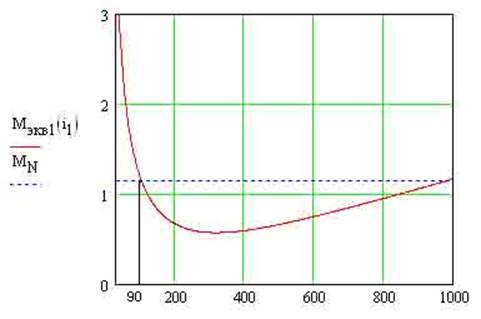
Рис.2.Графики Me(i), Mn.

Чтобы найти оптимальное значение передаточного числа редуктора, берем первую производную от следующего выражения:

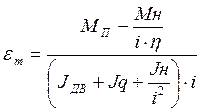
Приравниваем первую производную к нулю и находим экстремум функции при i_ОПТ=190

Графики функций номинального момента Мn, эквивалентного момента Me(i) и ускорения ε(i) представлены на рис.3.

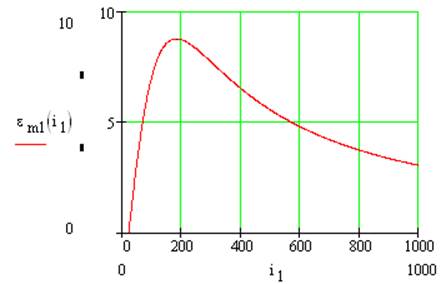
Рис.3. Графики Мn, Me(i), ε(i).

Полученное значение передаточного числа больше, рассчитанного раннее.

Поэтому, чтобы не увеличивать массогабаритные размеры и инерционность редуктора, оставляем передаточное число i=210

3.2 Расчетные формулы.

Для электропривода малой и средней мощности редуктор рассчитывается по следующим соотношениям.

Число пар зубчатых колес определяется по формуле:

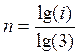              (6)

Затем определяем передаточное число каждой пары, исходя из того, что:

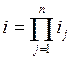
Чтобы обеспечить минимум момента инерции, для первых двух пар зубчатых колес подбирается передаточное число в пределах 2÷3, для остальных пар передаточное число выбирается в пределах 4÷8.

Число зубцов колеса определяется по формуле:

   ,           (7)

где z_2n-1 – число зубцов нечетного (ведущего) колеса.

Модуль определяется по формуле:

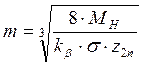 ,       (8)

где k_β – коэффициент ширины зуба, k_β=0.4÷0.6,

σ- напряжение в материале колеса,

z_2n – число зубов выходного колеса.

Диаметр колеса считается по формуле:

d_j=m·z_j         (9)