Расчет оптимального передаточного отношения редуктора. Расчет основных параметров редуктора, страница 5

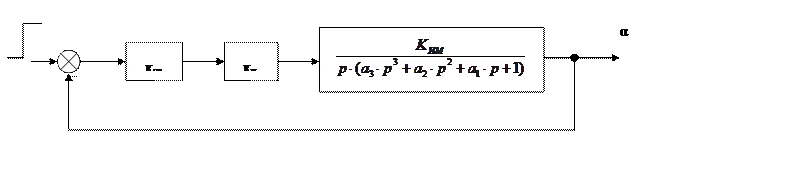
Рис. 11 Приведенная структурная схема привода антенны.

Из структурной схемы, приведенной на рисунке 11 , получается следующая передаточная функция для привода антенн:

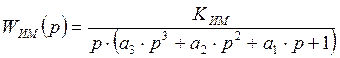
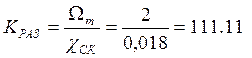
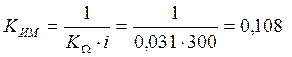
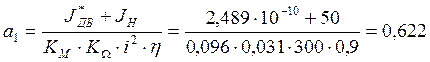
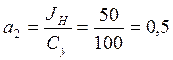
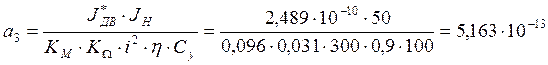
Рис. 12 Структурная схема привода антенн в

программной среде Matlab.

Рассматривается система в малых отклонениях.  На входе системы –функция единичного скачка, которая  эквивалентна поступлению на вход системы сигнала управления на поворот на один радиан.

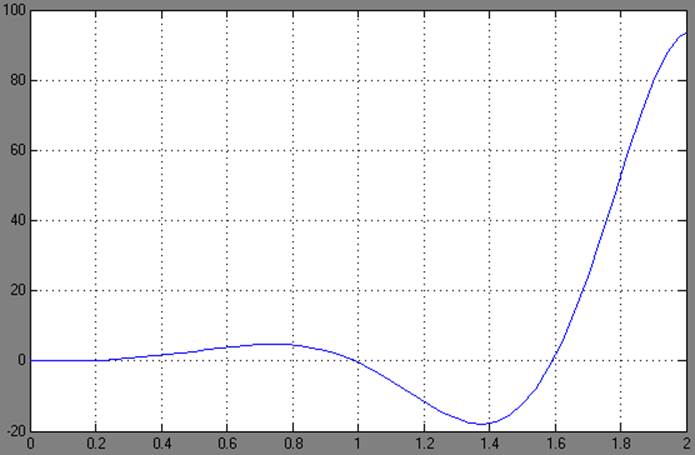
Рис. 13 График переходного

 процесса нескорректированной системы.

Для построения корректирующего звена необходимо представить передаточную функцию исходного звена в другом виде, при котором в знаменателе стоят элементарные сомножители.

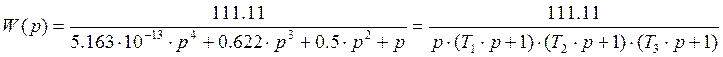
После решения знаменателя относительно p были найдены корни:

p₁=0

p₂=-0.4019296-j1.202568

p₃=-0.4019296+j1.202568

p₄=-1204725934533.3816925

Т₁=8,301·10^-13, Т₂=0,789 с,  .

Для привода антенн, запретная область в низкочастотной части ЖЛАХ строится по контрольной точке с координатами  и L().

Частота  определяется по формуле:

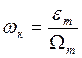, с^-1

где  - максимальное угловое ускорение, с^-2;

- максимальная угловая скорость, с^-1.

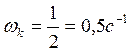
Амплитуда  определяется по формуле:

,

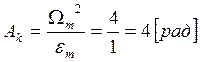Ордината контрольной точки определяется из соотношения:

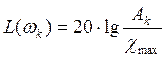
 – допустимая ошибка:

Получим:

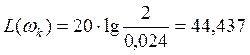
Точка пересечения правой границы запретной зоны с осью называется базовой частотой  и определяется по выражению:

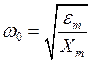, с^-1      

где     - наибольшее угловое ускорение, с^-2;

- амплитуда ошибки, рад;

Запретная область показана на рисунке пунктирной линией.

где     М – показатель колебательности;

- базовая частота, с^-1.

По выражению , получаем:

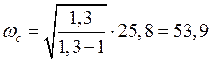, с^-1.

Через точку проходит участок ЖЛАХ с наклоном –20 дБ/дек, ограниченный слева частотой , а справа – частотой , определяемыми по следующим неравенствам соответственно:

;          

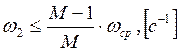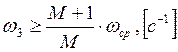;         где     М – показатель колебательности, - частота среза, с^-1.

Получаем:

Частота  соответствует точке пересечения среднечастотного участка с низкочастотным. Высокочастотная часть ЖЛАХ не должна заходить в запретную область, образованную асимптотой с наклоном –20 дБ/дек, пересекающей ось частот в точке  и горизонтальной прямой, соответствующей выражению:

,         

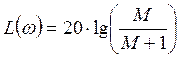Получаем:

.

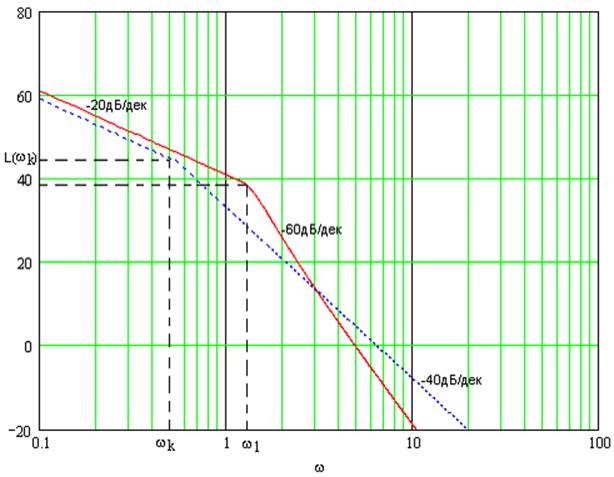
Рис. 14 ЛАХ нескорректированной передаточной функции с запретной областью.

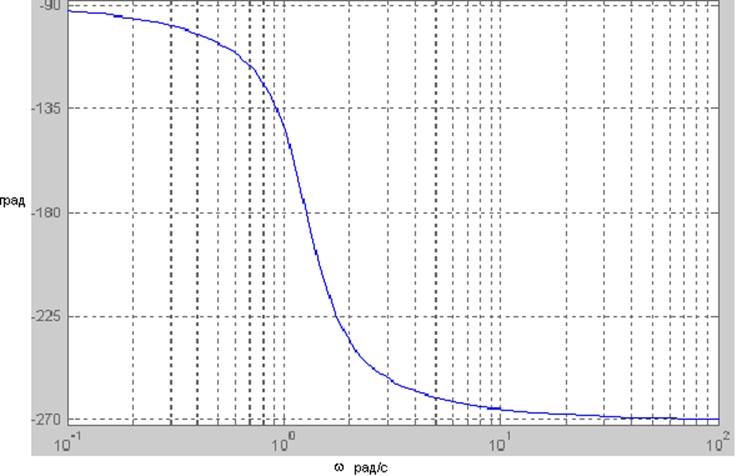
Рис. 15 ЛФХ нескорректированной передаточной функции.

Как видно из графика, данная ЛАХ заходит в запретную зону, ограниченную точкой L(ω_к). Кроме того, пересечение оси абсцисс идет под наклоном -60дБ/дек и происходит это в момент достижения  ЛФХ значения -180⁰ (система находится на грани устойчивости).

Для того чтобы система была устойчива необходимо  выполнить следующие условия:

- ЛАХ системы должна лежать выше контрольной точки L(ω_к),

- ЛАХ должна пересекать уровень 0дБ с наклоном -20дБ/дек,

- ЛАХ должна пересекать уровень 0дБ раньше, чем ЛФХ достигнет значения -180⁰.

Для того чтобы выйти из запретной зоны, ввод  дополнительного коэффициента усиления  не требуется, поскольку ЛАХ нескорректированной системы лежит выше контрольной точки. Так как система является астатической первого порядка, то первоначальный наклон ЛАХ составляет -20дБ/дек. В точке, соответствующей частоте 1.26 рад/с, происходит изменение наклона ЛАХ до -60дБ/дек. Для прохода уровня 0дБ с наклоном ‑20дБ/дек на частоте 2 рад/с изменим наклон ЛАХ на +40дБ/дек, затем после прохода уровня 0дБ – изменим наклон на ‑40дБ/дек на частоте 90 рад/с. Данная частота выбрана из необходимости получения нужного коэффициента колебательности М (длина участка 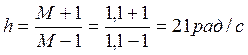).. Желаемая,   располагаемая ЛАХ, а также запретная область и ЛАХ корректирующего звена приведены на рис. 16. Желаемая ЛФХ – на рис. 17.