Расчет оптимального передаточного отношения редуктора. Расчет основных параметров редуктора, страница 2

Возьмем в качестве исходного, двигатель серии МИГ-180ДТ c параметрами приведенными в таблице 1.

Рн,	Ωн,	Jя,	Мп,	Мн,	Uун,	Iун,	Мтр,	Масса,
180	600	1,7·10-5	2,58	0,286	27	9,2	0,0286	5,7

Таблица 1.

Параметры двигателя МИГ-180ДТ.

Результирующий момент сопротивления движения можно определить с помощью метода эквивалентного рабочего цикла, который основывается на гипотезе о гармоническом характере движения вала. В этом случае результирующий момент сопротивления будет выглядеть:

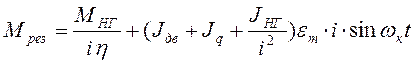
η – КПД редуктора выбирается равным (0,8-0,9).

i – коэффициент передачи редуктора, предварительно вычисляется по формуле: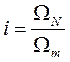

J_q – момент инерции редуктора, принимаем равным нулю, так как на данном этапе расчета параметры редуктора неизвестны.

sin(ωt) = 1, так как для проверки двигателя необходимо использовать максимальное значение результирующего момента.

Результирующий момент и пусковой момент двигателя должны удовлетворять условию:        

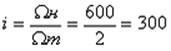
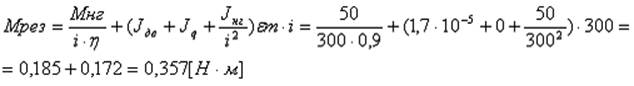
Условие  выполняется.

Данное условие является необходимым, но недостаточным для окончательного вывода о пригодности выбранного двигателя, так как момент нагрузки с течением времени может меняться, и средняя загрузка по току в течение всего времени работы может превысить номинальное значение, что будет приводить к перегреву двигателя. Поэтому момент сопротивления движению оценивается по значению эквивалентного момента:

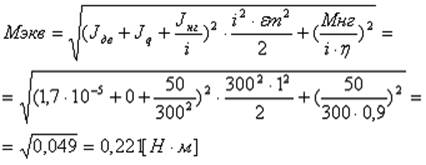
Номинальный момент двигателя больше эквивалентного , следовательно, двигатель серии МИГ-180ДТ удовлетворяет необходимому и достаточному условиям и окончательно выбран  в качестве исполнительного двигателя для систем автоматики. Двигатель серии МИГ-180ДТ  выполняется с гладким якорем, возбуждением от постоянных магнитов и тахогенератором. Управление двигателем осуществляется с помощью изменения напряжения якорной цепи. Чертеж двигателя с габаритными размерами приведен на рис. 1

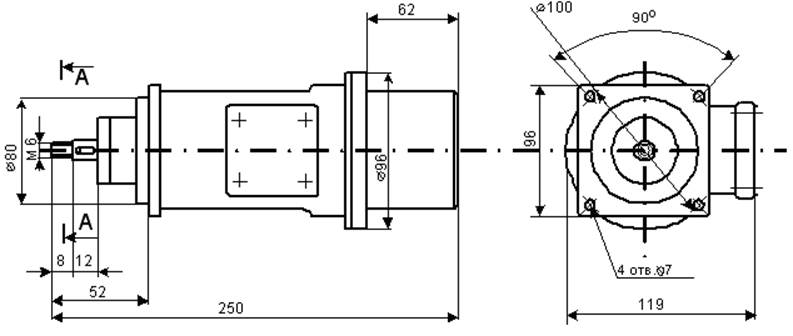
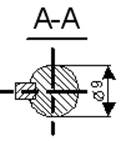
Рис. 1 Двигатель МИГ-180ДТ

3. Расчет оптимального передаточного отношения редуктора.

Предварительно определенное передаточное число может оказаться неоптимальным с точки зрения быстродействия системы, следовательно, это значение требует уточнения.

Для этого нужно построить графики  и прямую номинального момента двигателя. Точки пересечения прямой с графиком дают и . Экстремум графика  дает оптимальное значение передаточного отношения, которое обеспечит максимальное значение углового ускорения. На рис. 2 график функции  и прямая.

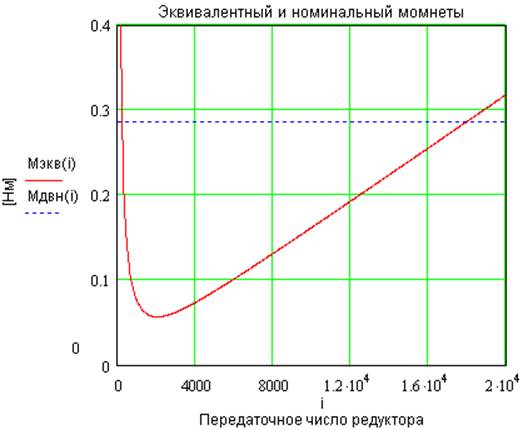
Рис. 2 Зависимость числа редуктора от

эквивалентного момента

После решения квадратного уравнения относительно i

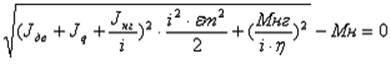 были найдены корни 231 и 23697. Следовательно, .

Взяв первую производную по  от уравнения 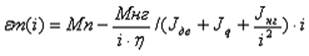 и приравняв ее к 0 получаем экстремум в точке . Эта точка лежит много правее, чем передаточное отношение , которое было сосчитано ранее. Выбираем окончательно передаточное отношение рис.4 так как с точки зрения инерционности системы увеличение передаточного отношения до максимального значения 1736 нежелательно и приведет к увеличению момента инерции редуктора и его массогабаритных показателей. На рис. 3 график функции .

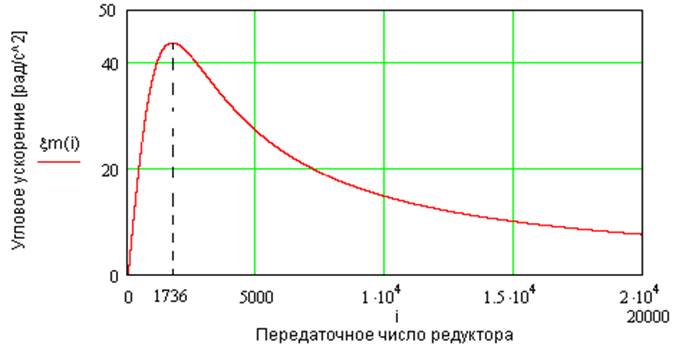
Рис. 3 Зависимость числа редуктора от углового ускорения

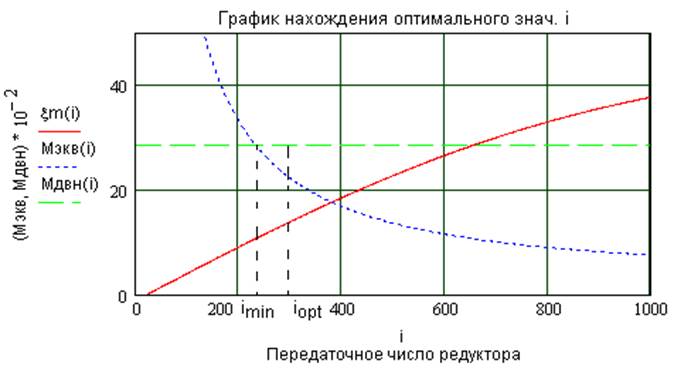
Рис.4

4. Расчет основных параметров редуктора.

Проведем расчет числа пар зубчатых колес:

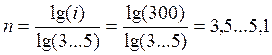, примем число пар 4.

Разобьем передаточное отношение редуктора на ряд передаточных отношений пар зубчатых колес по формуле:

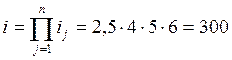
Выберем число зубцов каждого зубчатого колеса:

1 пара Z1=20, Z2=50

2 пара Z3=17, Z4=68

3 пара Z5=17, Z6=85

4 пара Z7=18, Z8=108