Другие предметы \ Железнодорожный путь

Проектирование реконструкции плана существующего пути в едином комплексе проектирования второго пути, страница 5

- второй кривой a2 – j2 =  29о13' –  2о19' = 26о54'.

Элементы проектируемого плана целесообразно представить в виде таблицы 4.1.

Т а б л и ц а  4.1 – Элементы проектируемого плана

Первая кривая

Вторая кривая

Третья кривая

a1 – Δa1 = 66о43'

R1 = 615 м

К1' = 716,12 м

Т1' = 404,88 м

Δa   = 4о34'

Rпр = 1500 м

Кпр = 119,55 м

Тпр = 59,81 м

a2 – Δa2  = 26о54'

R2 = 675 м

К2' = 316,91 м

Т2' = 161,43 м

Длины участков кривых, которые «отрезаются» от первой и второй существующих кривых, составят  (см. рисунок 4.4):

k 1 = 740,27 – 716,12 = 24,15 м;

k 2 = 344,20 – 316,91 = 27,29 м.

Определение пикетажного значения начала и конца проектируемых круговых кривых и истинной длины реконструируемого участка представлены в табличной форме – таблица 4.2.

Т а б л и ц а  4.2 – Результаты расчетов

Первая кривая

Вторая кривая

Истинная длина реконструируемого участка

ККс1……ПК 68+76,03

–k1…………   24,15

НКс2 ……ПК69+44,03

+k2……………   27,19

ККрек…..ПК69+71,32

– НКрек…ПК68+51,88

НКрек …..ПК68+51,88

ККрек…….ПК69+71,32

Кпик……………119,44

Величина неправильного пикета определится разностью длин Кпр  и Кпик:

Кпр …………………119,55

–Кпик………………. 119,44

DL                                 +0,11 

Неправильный пикет 100,11 м.

Определение нормалей в промежуточных точках

Для определения нормалей строится профильная схема и угловая диаграмма плана линии реконструируемого участка (рисунок 4.5), определяются коэффициенты tgj/2 и производится их увязка.

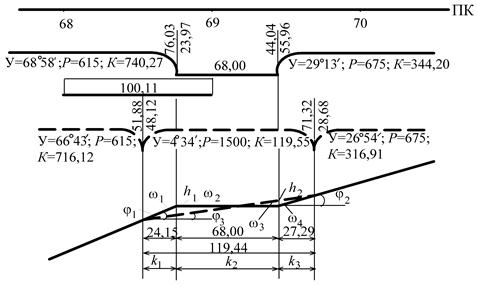
Рисунок 4.5 – Профильная схема плана реконструируемого

         участка и угловая диаграмма

Производится контроль расстояний (см. рисунок 4.5):

24,15 + 68,00 + 27,29 = 119,44 м.

tgj1 = 1/R1 = 1/615 = 0,00162602;  q1 = tg j1/2 = 0,00081301;

tgj2 = 1/R2 = 1/675 = 0,00148148;  q2 = tg j2/2 = 0,00074074;

tgj3 = Δa рад/ Кпр = 0,079703/119,44 =0,00066731; q3 = tgj3/2 =0,00033365;

Δ q1 = q1 − q3 = 0,00081301 – 0,00033365 = 0,00047936;

Δ q2 = q2 − q3 = 0,00074074 – 0,00033365 = 0,00040709;

h1 = Δa1  − k 1tgj3 = 0,039270 – 24,15 · 0,00066731 = 0,023155 м;

h2 = Δa2  – k 2tgj3 = 0,040433 – 27,29 · 0,00066731 = 0,022222 м;

k 3 = h1/ tgj3 = 0,023155/0,00066731 = 34,70 м;

k 4 = dс − k3 = 68,00 – 34,70 = 33,30 м;

ω1 = (k 1/2) h1 = (24,15/2) · 0,023155 = 0,28 м;

ω2 = (k 3/2) h1 = (34,70/2) · 0,023155 = 0,40 м;

ω3 = (k 4/2) h2 = (33,30/2) · 0,022222 = 0,37 м;

ω4 =  (k2/2) h2 = (27,29/2) · 0,022222 = 0,30 м.

Определяется невязка:

ω = ω1 + ω2 – ω3 – ω4 = 0,28 + 0,40 – 0,37 – 0,30 = 0,01 м.

Из-за малой величины невязкой можно пренебречь.

Формулы для расчета нормалей и подсчет нормалей представлены в таблице 4.3.

Т а б л и ц а  4.3 – Подсчет нормалей

Пикетаж

Исходное междупутье

Формула расчета

Нормаль, м

ПК

+

лево

право

68

60

80

0

0,68

+8,122 Δ q1= 0,03

–30,732q3= –0,31

0,03

0,37

69

20

40

60

80

0,68

0,68

0,68

0

0

–10,732q3= –0,04

–9,272q3= –0,03

–29,272q3= –0,29

+11,322 Δ q2= 0,05

0

0,64

0,65

0,39

0,05

0

70

0

0

0

4.3 Устройство новой кривой взамен прямой вставки, одной из

       кривых и части второй кривой

Такая реконструкция производится в том случае, когда одна из кривых имеет большую длину и от нее можно отсечь часть, а длина другой кривой незначительна.

Решение указанной задачи производится при наличии следующих данных: радиусов существующих кривых R1 и R2, длины существующей прямой вставки dс и угла поворота второй кривой a2. Радиус проектируемой кривой Rпр принимается.

На основании этих исходных данных определяются:

g – угол поворота новой кривой;

j – угол, отсекаемый от большой кривой;

b – смещение тангенса новой кривой относительно конца короткой кри вой.

Здесь возможны два случая: R1 < R2 и R1 > R2.

В первом случае проектируемый путь располагается снаружи существующей кривой, во втором случае – внутри, причем существующий путь смещается к центру.

Первый случай (R1<R2).

Значение радиуса новой кривой Rпр (рисунок 4.6) принимается с учетом  необходимости сдвижки тангенса b в сторону вершины угла (во избежание «противошерстной» сдвижки).

Величины искомых углов и сдвижки определяются из выражений:

    cos g = (Rпр – Бcos a2)/B;

      j= g -a2;

b = (А/ cosa2 + Т2) – (Бsin a2 + Вsin g),

(4.33)

(4.34)

(4.35)

где                                            А = dс + Т2;

               Б = R1 + Аtg a;

              В = Rпр – R1.

(4.36)

(4.37)

(4.38)

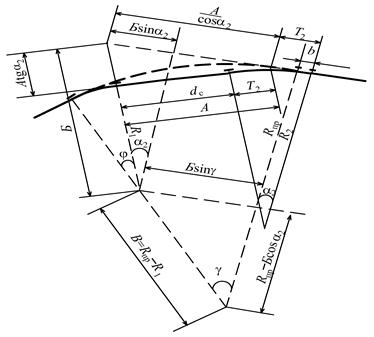
Рисунок 4.6 – Замена прямой вставки, малой и части

большой кривых одной общей кривой

Второй случай ( R1>R2):

            cos g = (Бcosa2 – Rпр)/B;

             j = g - a2;

b = Бsin a2 – (А/ cos a2 + Т2 + В sin g),

(4.39)

   (4.40)

(4.41)

где А и Б – те же величины;

                В = R1 + Rпр.

(4.42)

Приведем пример расчета увеличения прямой вставки указанным способом при следующих исходных данных:

первая кривая                                                  вторая кривая

a1 = 30о00' ;                                                       a2 = 16о00';

R1 = 800 м  ;                                                       R2 = 300 м;

К1 = 418,88 м;                                                   К2 = 83,78 м;

Т1 = 214,36 м;                                                   Т2 = 42,16 м;

начало кривой – ПК26 + 37,48;                       начало кривой – ПК30 + 92,36;

конец кривой  – ПК30 + 56,36;                        конец кривой  –  ПК31 + 76,14.

Длина существующей прямой вставки dс = 36,00 м. Требуется вместо недостаточной прямой вставки, малой кривой и части большой кривой вставить новую кривую радиусом  Rпр = 600 м.

Аналитический расчет

Аналитический расчет производится в соответствии со схемой, представленной на рисунке 4.7.

Определяем тригонометрические функции кривой малого радиуса:

Скачать файл