снижении ставок единого социального налога до 26 % Расходы, связанные с арендной платой, в 2003 г. составили 10,7 %, в 2004 г. этот процент увеличился на 1,1 и составил 11,8 %, а в 2005 г. произошло снижение данного показателя на 7,3 % и составил 4,5 %. Это связано с тем, что за период с 2003 по 2005 г. г. произошли изменения норм, ставок, тарифов арендуемой площади и арендной платы. Расходы на обязательные страховые платежи в 2003 г. составляли 1,0 %, в 2004 г. этот процент увеличился на 0,1 и составил 1,1 %, а в 2005 г. произошло увеличение данного показателя на 0,4 и составил 1,5 %. Это произошло за счет того, что на предприятиях стали уделять больше внимания страхованию своего персонала, страхованию собственных транспортных средств и выделять средства на данные расходы. Расходы, связанные с налогами и сборами, включаемыми в себестоимость продукции в 2003 г. составляли 3,1 %, в 2004 г. этот процент снизился на 1,3 и составил 1,8 %, в 2005 г. этот показатель также снизился на 1,2 и составил 0,6 %. Это произошло за счет снижения ставок налогообложения. Расходы по статье оплата услуг сторонних организаций в 2003 г. составляли 15,2 %, в 2004 г. этот показатель увеличился на 2 % и составил 17,2 %, а в 2005 г. этот процент снизился на 11,4 и составил 5,8 %. Показатели по остальным статьям расходов остались без заметных изменений.
В ходе анализа планов выполнения по товарообороту и издержкам наблюдается увеличение показателя товарооборота за период 2003-2005, а по издержкам в целом наблюдается снижение по отдельным статьям за период 2003-2005[111] .
Экономико-математическая модель - это отображение в виде совокупности уравнений, неравенств, логических отношений, графиков условного образа объекта для упрощения его исследования.
Экономико-математические модели позволяют выявить особенности функционирования экономического объекта и на основе этого прогнозировать его поведение при изменении каких-либо параметров.
Различают следующие виды экономико-математических моделей:
1) линейная:
· прямая;
· обратная;
2) гиперболическая;
3) параболическая;
4) логическая.
Для того, чтобы наиболее точно изучить влияние факторов на определенный объект, и наглядно проследить динамику этих изменений, наиболее оптимальным будет построение линейной модели.
Планирование издержек производства и обращения на предприятиях питания должно опираться на экономико-математический анализ.
Для анализа влияния товарооборота общественного питания на затраты на производство и реализацию продукции, необходимо построить экономико-математическую модель.
[112]
|
2005 |
||||
|
Т.О (Y) |
||||
|
Издержки |
Простейшей формой зависимости между переменными является линейная зависимость, и оценивание ее индикаторов и параметров является одним из важнейших направлений приложения математической статистики.
Прямолинейная зависимость двух переменных, отражается с помощью уравнения прямой:
Y= aX + b, (2.5)
где a, b – неизвестные коэффициенты зависимости;
X – независимая переменная;
Y– зависимая переменная.
Для расчетов параметров уравнения прямой однофакторной зависимости необходимо составить таблицу. 2.3
Табл. 2.3
Исходные и расчетные данные для определения параметров однофакторного уравнения прямой линейной связи
|
Годы |
Издержки производства и обращения, млрд. руб., Х |
Товарооборот, млрд. руб.,Y |
dх |
dy |
|
2003 |
19,8 |
69,4 |
- |
- |
|
2004 |
21 |
78,1 |
1,0607 |
1,1254 |
|
2005 |
27,1 |
104,4 |
1,2905 |
1,3368 |
Зависимость между издержками производства и обращения и товарооборотом можно проследить на рис. 2.1.
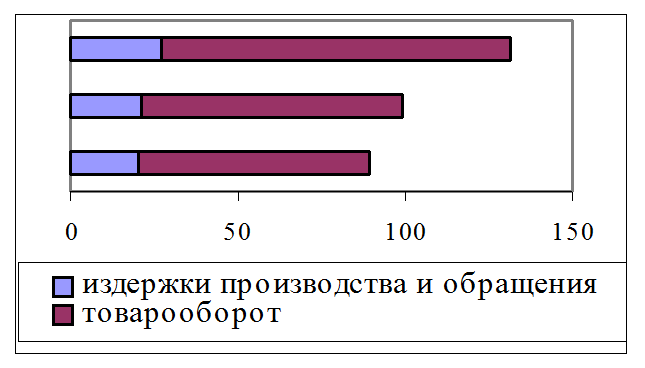 |
Рис. 2.1 Зависимость между издержками производства и обращения и товарооборотом
В ходе расчетов был получен коэффициент[113] , равный 1,0607. Данный коэффициент свидетельствует о том, что изменение размеров отклонений коэффициентов сравнения факторного признака на единицу, приводит к изменению размера отклонения коэффициентов сравнения результативного признака в 1, 0607 раза[114] .
В ходе расчетов было выявлено, что наиболее оптимальной является применение линейной модели[115] [116] .
Вычислим коэффициент корреляции.
Расчет коэффициента корреляции определяется по формуле:
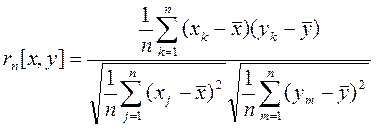 , (2.5)
, (2.5)
Расчеты коэффициента корреляции представлены в табл. 2.4.
Табл. 2.4
Расчеты коэффициента корреляции
|
Коэффициент корреляции |
||
|
dxdy |
dx2 |
dy2 |
|
1,19371 |
1,42494 |
1,26653 |
|
1,8869 |
1,6659 |
1,7869 |
|
Итого |
3,0904 |
3,0436 |
По данным табл. 2.4 коэффициент корреляции составит гху— 0,6615. Коэффициент корреляции важен для исследования экономических явлений и процессов. Он принимает значения в интервале: - 1 <гху< 1.
Табл. 2.5
Критерий оценки устойчивости связи между экономическими явлениями
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.