Гидрогазодинамика
Содержание:
1. Формулы Вейсбаха и Вейсбаха-Дарси для определения гидравлических потерь. (2-3)
2. Влияние режима движения и шероховатости стенок на коэффициент гидравлического трения.(3-5)
3. Уравнение Эйлера для турбомашин. (6)
4. Пересчет характеристик насоса на разные частоты вращения. (7-8)
5. Работа насоса на простой трубопровод. (9)
6. Уравнение Бернулли для потока сжимаемой жидкости. (9-10)
7. Связь между полными и статическими параметрами в газовом потоке.(10)
8. Течение жидкости в криволинейном канале.(10-12)
9. Расчет трубопроводов с параллельными ветвями.(12-15)
10. Условие отрыва пограничного слоя от криволинейной поверхности. (16)
11. Кинематика потока в рабочем колесе центробежного насоса и компрессора.(16-18)
1. Формулы Вейсбаха и Вейсбаха–Дарси для определения гидравлических потерь.
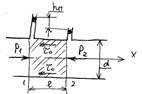
Рассмотрим
равномерное течение реальной жидкости в трубе диаметром ![]() причем
ось
причем
ось ![]() направлена по оси трубы в сторону
движения.Выделим нормальное сечение
направлена по оси трубы в сторону
движения.Выделим нормальное сечение ![]() часть потока
часть потока ![]() и рассмотрим ее равновесие в
проекции на ось
и рассмотрим ее равновесие в
проекции на ось ![]()
Потери напора на трение связаны с силами трения между жидкостью и внутренними стенками трубы, а также с силами трения между слоями жидкости.
Обозначим
касательные напряжения на внутренней стенке трубы через ![]()
Потери напора на
участке ![]() будут равны:
будут равны: ![]() (1)
(1)
Из условия
равновесия объема жидкости сумма проекций всех сил на ось ![]() должна быть равна
должна быть равна ![]()
Обозначим площадь
нормального сечения через ![]() а периметр –
а периметр – ![]()
Тогда условие равновесия: ![]() Отсюда
Отсюда ![]() (2)
(2)
Подставив ![]() из (2) в (1),
получим
из (2) в (1),
получим ![]() (3)
(3)
Обозначим величину
![]() гидравлическим диаметром. Для трубы
круглого сечения
гидравлическим диаметром. Для трубы
круглого сечения ![]()
Тогда ![]() (4)
(4)
Выражение для
касательных напряжений ![]() найдем из теории подобия.
Возникающая на внутренней стенке трубы касательная сила
найдем из теории подобия.
Возникающая на внутренней стенке трубы касательная сила ![]() будет
равна:
будет
равна: ![]()
![]() (5)
(5)
где ![]() коэффициент
трения на внутренней стенке трубы, который является функцией числа Рейнольдса:
коэффициент
трения на внутренней стенке трубы, который является функцией числа Рейнольдса: ![]()
Подставив (5) в
(4): ![]() (6)
(6)
Величина ![]() называется коэффициентом
сопротивления трения или коэффициентом гидравлического трения (коэффициент
Д’Арси).
называется коэффициентом
сопротивления трения или коэффициентом гидравлического трения (коэффициент
Д’Арси).
Тогда окончательное выражение для потерь напора на трение запишется в виде:
![]() (7)
(7)
Формула (7) может
быть записана в виде: ![]() (7´)
(7´)
Экспериментально
доказано, что ![]()
Для ламинарного режима течения
потери напора определяются по формуле Пуазейля:![]()
Преобразуем эту
формулу, домножив числитель и знаменатель на ![]() с
учетом выражения (7):
с
учетом выражения (7):
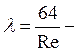 формула Стокса. (8)
формула Стокса. (8)
Законы сопротивления при ламинарном и турбулентном
режимах течения отличаются, если для ламинарного режима hп V (ф-ла
Пуазейля), то при турбулентном режиме hп V2. При переходе к турбулентному режиму течения при своем
поперечном перемещении частицы жидкости перемещается из менее подвижного слоя в
более подвижный, в результате чего в жидкости возникает вращательное движение
которое служит причиной возникновения вихрей. Поэтому при турбулентном режиме
имеет место вихревой механизм потерь, и величина потерь определяется по формуле
Вейсбаха 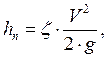 где
где ![]() -безразмерный коэффициент
сопротивления, который определяется экспериментально.
-безразмерный коэффициент
сопротивления, который определяется экспериментально.
2. Влияние режима движения и шероховатости стенок на коэффициент гидравлического трения.
 В
технике гладких труб не бывает, все трубы являются шероховатыми.
В
технике гладких труб не бывает, все трубы являются шероховатыми. ![]() -относительная шероховатость трубы.
Для труб она является критерием
-относительная шероховатость трубы.
Для труб она является критерием
геометрического подобия, т.е. для геометрически
подобных труб 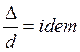 .
.
Эксперимент
показывает, что в общем случае для шероховатых труб: 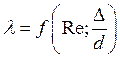 .
.
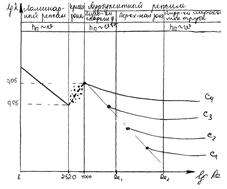
Турбулентное течение в трубах делят на зоны, зависящие
от физических особенностей процесса течения и характера зависимости ![]() от критериев подобия: а) гидравлически-гладкие
трубы; б) гидравлически-шероховатые трубы.
от критериев подобия: а) гидравлически-гладкие
трубы; б) гидравлически-шероховатые трубы.
В гидравлически-гладких трубахшероховатость полностью покрыта ламинарным подслоем.
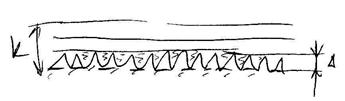
![]() . Для
таких труб
. Для
таких труб ![]() =f(Re)
=f(Re)
Для этой зоны экспериментально
получены эмпирические зависимости: 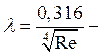 формула
Блайзера, которая справедлива в этом интервале:
формула
Блайзера, которая справедлива в этом интервале: ![]()
Формула
Конакова: 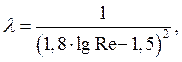 которая справедлива в
интервале:
которая справедлива в
интервале: ![]()
Верхняя граница гидравлически-гладкой
зоны: 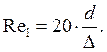 С увеличением числа Рейнольдса
С увеличением числа Рейнольдса ![]() уменьшается. Это обусловлено
наличием ламинарного подслоя и его свойствами.
уменьшается. Это обусловлено
наличием ламинарного подслоя и его свойствами.
Re
![]()
3000 0,05
104 0,03
105 0,02
106 0,01
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.