При
расчете сложных трубопроводов с большим количеством параллельных ветвей ![]() применяют метод эквивалентных
труб.
применяют метод эквивалентных
труб.
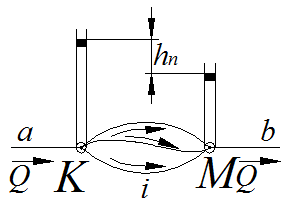 Обозначим через
Обозначим через ![]() порядковый номер
одной из параллельных ветвей.
порядковый номер
одной из параллельных ветвей.
Потери напора в параллельных ветвях:
![]() (5)
(5)
Магистральный расход равен сумме расходов в параллельных ветвях:
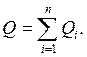 (6)
(6)
Рисунок 20.2 – Схема участка трубопровода
с параллельными ветвями
 Равенство потерь напора в параллельных ветвях соответствует
выражению:
Равенство потерь напора в параллельных ветвях соответствует
выражению:
![]() (7)
(7)
Пусть
![]() эквивалентная труба, создаваемая при
том же магистральном расходе
эквивалентная труба, создаваемая при
том же магистральном расходе ![]() такие же потери
напора
такие же потери
напора ![]()
Сопротивление
эквивалентной трубы обозначим через ![]() тогда для этой
трубы получим:
тогда для этой
трубы получим:
![]() (8)
(8)
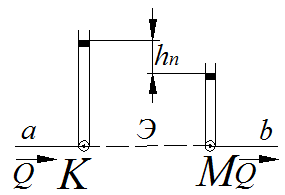
Рисунок 20.3 – Схема участка трубопровода
с эквивалентной трубой
Из
(5) следует, что 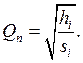
Из (6) и (8)
следует, что 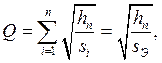 отсюда следует, что
отсюда следует, что 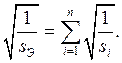 (9)
(9)
Баланс напоров для
данного трубопровода: ![]() (10)
(10)
Решая
полученную систему уравнений, находят значения магистрального расхода ![]() и расхода в ветвях
и расхода в ветвях ![]()
Задача по расчету трубопровода с параллельными ветвями может быть решена также графическим способом.
Построим
в координатах ![]() суммарную характеристику
параллельных ветвей
суммарную характеристику
параллельных ветвей ![]() и
и ![]() используя
(1) и (2), путем сложения абсцисс (расходов) при одинаковых ординатах (потери
напора).
используя
(1) и (2), путем сложения абсцисс (расходов) при одинаковых ординатах (потери
напора).
Полученная
суммарная характеристика разветвленного участка и будет характеристикой трубы ![]()
1) Проводим рад
вспомогательных линий ![]()
2) и т. д.
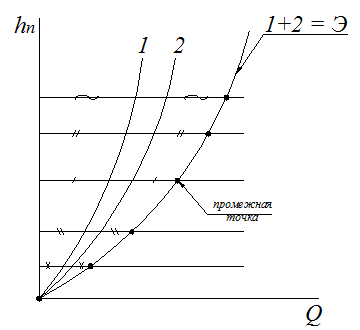 Построим характеристику для трубопровода с параллельными
участками в целом, включая и характеристики магистральных участков.
Построим характеристику для трубопровода с параллельными
участками в целом, включая и характеристики магистральных участков.
1)
Проводим характеристику участков ![]() и
и ![]()
2) при сложении этих характеристик используем уравнение (3);
3)
так как через магистральные участки ![]() и эквивалентную
трубу
и эквивалентную
трубу ![]() проходит один и тот же расход
проходит один и тот же расход ![]() будем складывать ординаты (напоры)
при одинаковых абсциссах (расходах).
будем складывать ординаты (напоры)
при одинаковых абсциссах (расходах).
4)
проводим ряд вспомогательных линий ![]()
5)
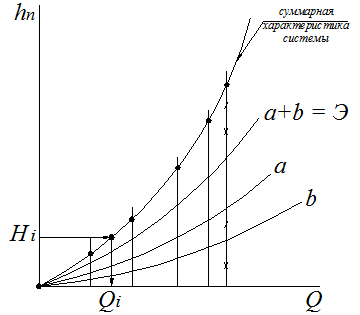
по суммарной характеристике системы для заданного напора ![]() получаем магистральный
получаем магистральный
Рисунок 20.4 – Схема графического расход ![]()
способа решения задачи по расчету
сложного трубопровода с параллельными
ветвями
10. Условие отрыва ПС от криволинейной поверхности.
Рассмотрим профили скоростей в потоке вязкой жидкости,
обтекающую криволинейную поверхность. В т. А,В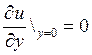
![]() по мере удаления от стенки
возрастает, а в т. С
по мере удаления от стенки
возрастает, а в т. С ![]() и
и ![]() .
.
Из
закона жидкостного трения Ньютона касательное напряжение в т.С 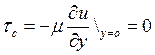 т.к
т.к 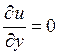 в
т.С. Математически условия отрыва ПС от криволинейной поверхности записывается
в виде
в
т.С. Математически условия отрыва ПС от криволинейной поверхности записывается
в виде 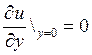 .
.
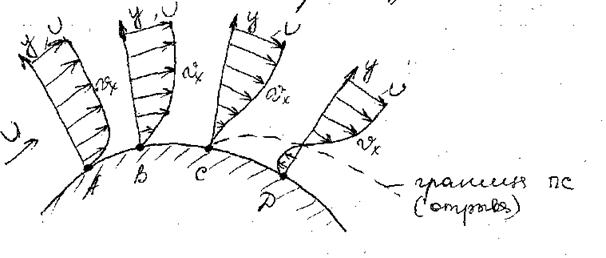 Потому
что жидкость перестает тереться о стенку в т. С и далее в ней возникают обратные
точки приводящие к преобразованию вторичных вихревых течений как в т.Д
Потому
что жидкость перестает тереться о стенку в т. С и далее в ней возникают обратные
точки приводящие к преобразованию вторичных вихревых течений как в т.Д
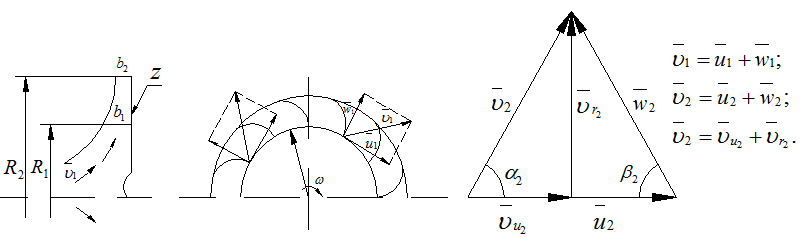
11. Кинематика потока в рабочем колесе центробежного насоса и компрессора.
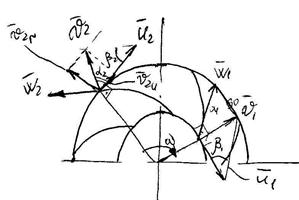 |
Рисунок 25.1 – Кинематика потока в рабочем колесе центробежного насоса
![]() осевая ширина лопатки на входе
рабочего колеса насоса;
осевая ширина лопатки на входе
рабочего колеса насоса;
![]() осевая ширина лопатки на выходе
рабочего колеса насоса.
осевая ширина лопатки на выходе
рабочего колеса насоса.
Для
неподвижного наблюдателя видно абсолютное движение жидкости со скоростью ![]() а для подвижного наблюдателя
(движущегося вместе с частицами жидкости) видно относительное движение жидкости
относительно стенок межлопаточного канала колеса по траектории, повторяемой
форму лопатки с относительной скоростью
а для подвижного наблюдателя
(движущегося вместе с частицами жидкости) видно относительное движение жидкости
относительно стенок межлопаточного канала колеса по траектории, повторяемой
форму лопатки с относительной скоростью ![]()
Кроме
того, жидкость участвует в переносном вращательном движении вместе с колесом с
окружной (переносной) скоростью ![]() Таким образом
абсолютная скорость
Таким образом
абсолютная скорость ![]() жидкости, движущейся в
рабочем колесе, складывается из относительной скорости
жидкости, движущейся в
рабочем колесе, складывается из относительной скорости ![]() и
окружной (переносной) скорости
и
окружной (переносной) скорости ![]()
![]()
Входное
сечение на лопатке колеса обозначается ![]() а
выходное сечение
а
выходное сечение ![]() Угол между относительной
скоростью и окружной скоростью называется углом лопатки
Угол между относительной
скоростью и окружной скоростью называется углом лопатки ![]() Угол между абсолютной скоростью
Угол между абсолютной скоростью ![]() и
и ![]() называется
углом потока
называется
углом потока ![]()
Абсолютная
скорость ![]() может быть представлена как
геометрическая сумма радиальной составляющей
может быть представлена как
геометрическая сумма радиальной составляющей ![]() и
окружной составляющей
и
окружной составляющей ![]()
Окружная
составляющая ![]() абсолютной скорости представляет
собой ее проекцию на направление окружной скорости, а радиальная составляющая
абсолютной скорости представляет
собой ее проекцию на направление окружной скорости, а радиальная составляющая ![]() проекцию вектора абсолютной скорости
на направление радиуса, соединяющего данную точку потока с осью вращения.
проекцию вектора абсолютной скорости
на направление радиуса, соединяющего данную точку потока с осью вращения.
В
центробежных насосах колеса делают с радиальным входом, т. е. абсолютная
скорость ![]() направлена вдоль радиуса,
проходящего через ось вращения рабочего колеса.
направлена вдоль радиуса,
проходящего через ось вращения рабочего колеса.
Тогда
для этого случая ![]() (по величине и направлению),
а угол потока
(по величине и направлению),
а угол потока ![]()
Обозначим
объемный расход жидкости через рабочее колесо через ![]() тогда
тогда
![]() из уравнения неразрывности
определяется через расход
из уравнения неразрывности
определяется через расход ![]()
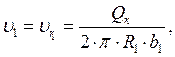
где
![]() осевая ширина лопатки на входе в
рабочее колесо;
осевая ширина лопатки на входе в
рабочее колесо;
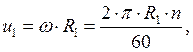
где
![]() частота вращения рабочего колеса,
частота вращения рабочего колеса, ![]()
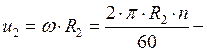 окружная скорость на выходе рабочего
колеса.
окружная скорость на выходе рабочего
колеса.
Закручивание
потока лопатками рабочего колеса служит мерой передачи энергии от лопатки к
частицам потока. Оно характеризуется окружной составляющей абсолютной скорости ![]() без наличия которой не было бы
передачи энергии от рабочего колеса жидкости.
без наличия которой не было бы
передачи энергии от рабочего колеса жидкости.
Радиальная составляющая абсолютной скорости на выходе рабочего колеса:
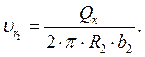
Турбокомпрессоры по характеру преобразования энергии наиболее близки к центробежным и осевым насосам. Эта общность ведет к сходным конструктивным формам и эксплуатационным характеристикам турбокомпрессоров и насосов. Различие между ними вызывается главным образом тем, что в турбокомпрессорах газ сжимается, а в турбонасосах рабочая среда практически не сжимается. Кроме того, поскольку плотность рабочей среды у турбокомпрессоров обычно на 2–3 порядка меньше, чем у насосов, для создания одинакового перепада давлений в компрессорах необходимо создать значительно бóльшие скорости движения как лопаток рабочего колеса, так и газа.
Таким образом видим, что кинематика потока в рабочем колесе центробежного насоса схожа с кинематикой потока в рабочем колесе центробежного компрессора.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.