трубопровод то ![]()
Построим
характеристику насоса для всех трех случаев и в точках пересечения этих
характеристик с характеристикой насоса получим величины ![]() и
и
![]() для каждого из случаев при
для каждого из случаев при 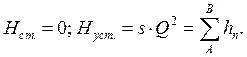
В
третьем случаи жидкость потечет из бака![]() в
бак
в
бак ![]() самотеком с расходом
самотеком с расходом ![]()
Применение
насоса в этом случаи позволяет получить объемный расход ![]()
6. Уравнение Бернулли для потока сжимаемой жидкости.
Для потока
идеальной не сжимаемой жидкости оно имеет вид 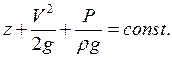
Т.к. в потоке сжимаемой
жидкости плотность вдоль струйки тока является переменной то уравнение Бернулли
для такого потока приобретает вид 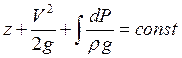 . В
газодинамических задачах
. В
газодинамических задачах 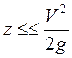 - можно пренебречь.
Тогда уравнение Бернулли примет вид
- можно пренебречь.
Тогда уравнение Бернулли примет вид 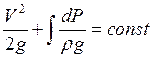 (1) . Из
уравнения адиабатного процесса
(1) . Из
уравнения адиабатного процесса 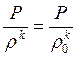 ,
, 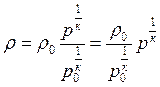
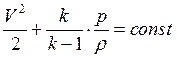 (2)
уравнение Бернулли для сжимаемой жидкости.
(2)
уравнение Бернулли для сжимаемой жидкости. 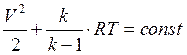 (3)
(3)
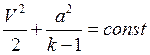 (4)
(4)
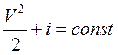 (5).
(5).
7. Связь между полными и статическими параметрами в газовом потоке.
Пусть газовый поток со скоростью V
попадает на твердую стенку. В точке О его скорость становится равной 0 (точка
торможения). Местная скорость звука в точке О будет равняться ![]() .
.
Запишем уравнение Бернулли для произвольного, и сечения
проходящего через точку торможения 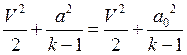 , разделим на
, разделим на ![]() . Получим
. Получим 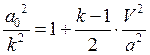 или
или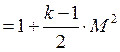 , где М-число маха (отношение
скорости потока к местной скорости звука).
, где М-число маха (отношение
скорости потока к местной скорости звука). 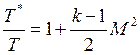 .
Т.к. течение является адиабатным
.
Т.к. течение является адиабатным 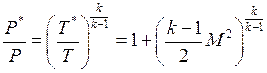 ,
, 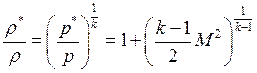 .
.
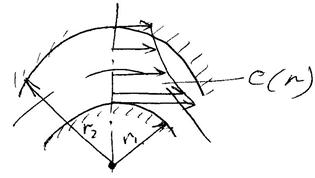
8. Течение жидкости в криволинейном канале.
Рассмотрим канал прямоугольного сечения глубиной «b», образованный радиусами r1 и r2 , по которому течет идеальная жидкость.
На радиусе r
выделим в потоке элемент объемом с угловым размером ![]() ,
радиальным
,
радиальным ![]() и массой
и массой ![]()
Рассмотрим условия равновесия этого элемента: на него действует центробежная сила
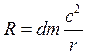 и
сила, действующая на элемент сверху и снизу,
и
сила, действующая на элемент сверху и снизу, ![]() .
.
Из условия равновесия данного
элемента 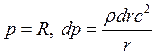
Уравнение Бернулли для
идеальной жидкости, отнесенное к единице объема, пренебрегая геометрическим
напором 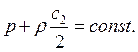
 Продифференцируем обе его
части по r:
Продифференцируем обе его
части по r: 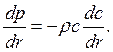
Разделяя переменные, получим 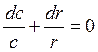 . Проинтегрировав
. Проинтегрировав 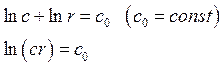
![]() (7)
закон распределения скорости вдоль радиуса в криволинейном канале.
(7)
закон распределения скорости вдоль радиуса в криволинейном канале.
Найдем объемный расход
жидкости через сечение канала: 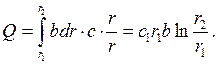
Найдем среднюю расходную скорость жидкости в криволинейном канале сср:
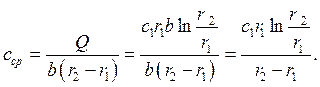
Радиус ![]() на
который расположена средняя скорость из формулы (7)
на
который расположена средняя скорость из формулы (7) 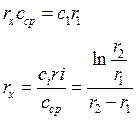
Выразим текущую через среднюю 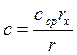 Подставим «с» в
Подставим «с» в 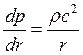
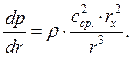
Проинтегрируем по r: 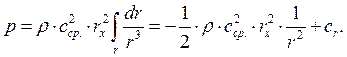
![]()
Постоянную ![]() найдем из граничных условий.
найдем из граничных условий.
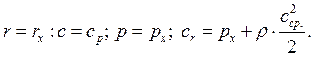
Подставляя ![]() в
в ![]()
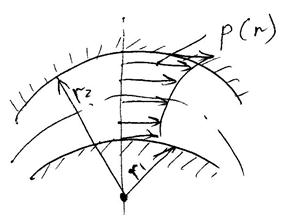
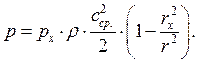 распределение
давления по r/
распределение
давления по r/
Полученные выражения ![]() и
и 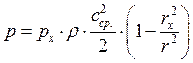 будут
справедливы и для течения через криволинейный канал круглого сечения, так как в
них не входит глубине канала b.
будут
справедливы и для течения через криволинейный канал круглого сечения, так как в
них не входит глубине канала b.
При движении в криволинейном канале реальной жидкости будут сказываться и влияние пограничного слоя.
Вихревая зона
Вблизи вогнутой стенки
жидкость движется замедленно 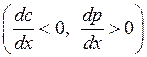 и образующаяся
зона 1 характеризуется срывом потока с образованием вихревого течения.
и образующаяся
зона 1 характеризуется срывом потока с образованием вихревого течения.
У выпуклой стенки
криволинейного канала также образовывается зона с уменьшением скорости 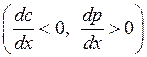 и образовывается зона 2, в которой
также происходит срыв потока с выпуклой стенки с образованием завихрений.
и образовывается зона 2, в которой
также происходит срыв потока с выпуклой стенки с образованием завихрений.
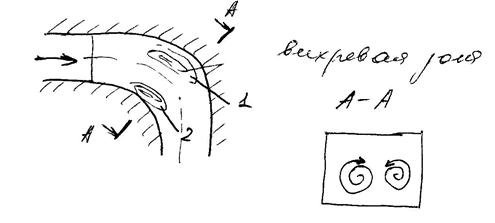 В результате в жидкости
нарушается радиальное равновесие и жидкость перетекает от вогнутой стенки, где
давление растет, т. е. возникает парный вихрь вторичного течения,
гидравлических потерь в потоке.
В результате в жидкости
нарушается радиальное равновесие и жидкость перетекает от вогнутой стенки, где
давление растет, т. е. возникает парный вихрь вторичного течения,
гидравлических потерь в потоке.
Для уменьшения этих потерь следует: 1) выполнять канал с некоторой конфузорностью; 2) увеличивать радиус кривизны канала.
Если в криволинейном канале течение протекает без срывов, то распределение скоростей и давлений по радиусу канала для реальной жидкости совпадает с их распределением для идеальной.
9. Расчет трубопроводов с параллельными ветвями.
Для решения задач по расчету сложных трубопроводов составляется система уравнений, которые устанавливают связь между параметрическими характеристиками потока жидкости в трубах (размерами труб, расходами и напорами).
Эта система состоит из уравнений баланса расходов для каждого узла и уравнений баланса напоров (уравнений Бернулли) для каждой ветви трубопроводов.
Для получения одного решения эта система должна быть замкнутой, т. е. число независимых неизвестных в ней должно быть равно числу уравнений.
Поскольку обычно сложные трубопроводы являются длинными в уравнениях Бернулли можно пренебрегать скоростными напорами считая, что полный напор потока в каждом сечении равен гидростатическому напору, который выражается высотой пьезометрического уровня над принятой плоскостью сравнения.
Кроме того, можно пренебречь относительно малыми местными потерями напора в узлах. Это позволяет в уравнениях Бернулли оперировать понятием потерь напора в каждом узле.
При расчетах сложных трубопроводов можно использовать электрогидравлическую аналогию, при которой:
– объемные расходы соответствуют токам:
– напоры и потери напоров соответствуют напряжению;
– гидравлические сопротивления соответствуют электрическим.
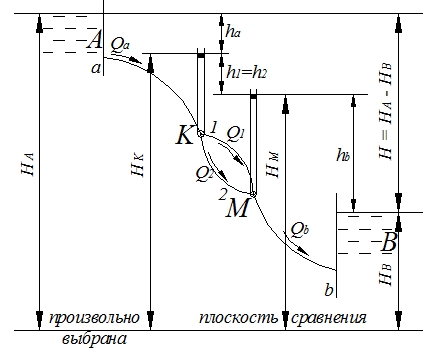 Жидкость из питателя
Жидкость из питателя![]() через
трубопровод с параллельными ветвями
через
трубопровод с параллельными ветвями ![]() и
и ![]() перетекает в приемник
перетекает в приемник ![]() Точки
Точки ![]() и
и
![]() являются узловыми, а участки
являются узловыми, а участки ![]() и
и ![]() магистральными.
Располагаемый напор
магистральными.
Располагаемый напор ![]()
Составляем систему расчетных уравнений:
1) Уравнение баланса расходов в узлах:
–
для узла ![]()
![]()
–
для узла ![]()
![]()
Из уравнения неразрывности следует:
![]() (1)
(1)
2) Уравнение равенства потерь напора в параллельных ветвях:
Рисунок 20.1 –
Схема сложного трубопровода обозначим через ![]() и
и
![]() потери напора в
потери напора в
с параллельными
ветвями магистральных участках ![]() и
и ![]()
![]() и
и ![]() потери
напора в параллельных ветвях
потери
напора в параллельных ветвях ![]() и
и ![]()
![]() и
и ![]() напоры
в узлах точек
напоры
в узлах точек ![]() и
и ![]()
Тогда
![]() отсюда следует, что
отсюда следует, что ![]()
Для
турбулентного режима потери напора определяются зависимостью: ![]()
где
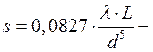 сопротивление трубы.
сопротивление трубы.
Так
как ![]() то
то
![]() (2)
(2)
3) Уравнение балансов напора в системе:
![]() или
или
![]() (3)
(3)
Считая
известными ![]() и
и ![]() получаем
систему из трех уравнений с тремя неизвестными
получаем
систему из трех уравнений с тремя неизвестными ![]() которая
является замкнутой.
которая
является замкнутой.
Распределение
расхода между параллельными ветвями ![]() и
и ![]() можно получить из (2):
можно получить из (2):
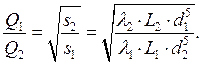 (4)
(4)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.