В гидравлически-шероховатых трубахнеровности шероховатости находятся в турбулентном ядре потока и обтекаются жидкостью с большими скоростями.
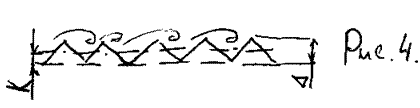
![]() ,
, ![]() =f(
=f(![]() )
)
Для этой зоны имеются эмпирические зависимости 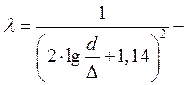 - формула Никурадзе.
- формула Никурадзе.
Нижняя граница
гидравлически-шероховатой зоны: 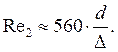 . Отношение
. Отношение ![]() называется гидравлической
гладкостью трубы. При возрастании гладкости
называется гидравлической
гладкостью трубы. При возрастании гладкости![]() уменьшается.
уменьшается.
![]() 50 102 103
104
50 102 103
104
![]() 0,05 0,04 0,02
0,01
0,05 0,04 0,02
0,01
Между гидравлически-гладкой и шероховатой зонами
находится переходнаязона, для которой ![]() . Для переходной зоны
. Для переходной зоны 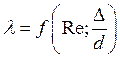 . Потери на трение в зависимости от
числа Re можно
представить графически в виде номограмм.
. Потери на трение в зависимости от
числа Re можно
представить графически в виде номограмм.
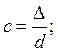
![]()
 В критической
зоне график терпит разрыв (большой разброс значений).
В критической
зоне график терпит разрыв (большой разброс значений).
|
геометрической форме, по расположению).
Имея заданную
величину ![]() можно подобрать искусственнуюшероховатость,
однородную по стенке канала и по сопротивлению эквивалентную данной
естественной шероховатости
можно подобрать искусственнуюшероховатость,
однородную по стенке канала и по сопротивлению эквивалентную данной
естественной шероховатости![]()
Для технически гладких
труб (стеклянных медных) ![]() =0,001-0,01 мм.
=0,001-0,01 мм.
Для технически шероховатых
труб ![]() =0,1-0,5 мм.
=0,1-0,5 мм.
Для технически шероховатых труб при турбулентном режиме
можно пользоваться эмпирической формулой Альтшуля: 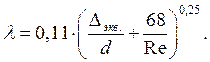
3. Уравнение Эйлера для турбомашин.
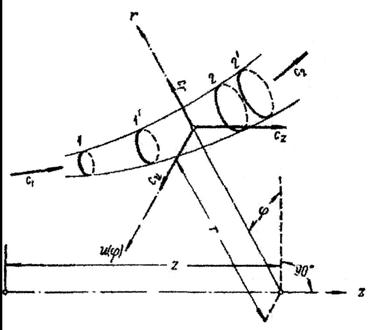
Рассмотрим
установившееся движение газа в струйке тока. Струйка тока произвольной формы
вращается с постоянной угловой скоростью ![]() относительно
оси
относительно
оси ![]() прямоугольной декартовой системы координат.
прямоугольной декартовой системы координат.
Объем газа в
струйке тока, ограниченный сечениями ![]() и
и
![]() за малый промежуток времени
за малый промежуток времени ![]() перемещается в положение
перемещается в положение ![]() Масса газа, заключенная в
объемах
Масса газа, заключенная в
объемах ![]() и
и ![]() равны
равны
![]()
Изменение момента импульса за время ![]() будет равно разности моментов
импульса для объема
будет равно разности моментов
импульса для объема ![]() и объема
и объема ![]()
![]()
Согласно закону сохранения импульса изменение момента импульса относительно некоторой неподвижной оси равно главному моменту всех внешних сил, приложенных к данной массе, относительно той же оси:
![]()
Умножив правую и левую части уравнения на
угловую скорость ![]() и разделив на массовый
расход
и разделив на массовый
расход ![]() получим:
получим:
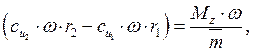
где 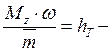 теоретический
(эйлеров) напор, который имеет размерность удельной энергии
теоретический
(эйлеров) напор, который имеет размерность удельной энергии ![]()
Так как ![]() то
получим уравнение Эйлера для турбомашин:
то
получим уравнение Эйлера для турбомашин: ![]()
Справедливо только для колес с радиальным входом на лопатки.
Уравнение Эйлера устанавливает связь между энергетическими показателями турбомашины и кинематическими параметрами потока газа в проточной части этой турбомашины. Данное уравнение используется при расчетах компрессоров, насосов и турбин.
4. Пересчет характеристик насоса на разные частоты вращения.
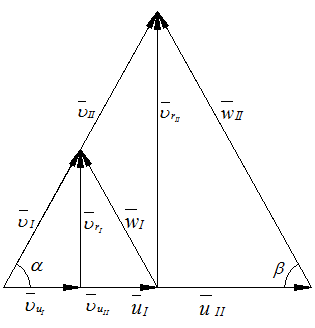
Этот пересчет основан на теории подобия.
Рассмотрим связанные с ней основные понятия:
1) подобные насосы – насосы, имеющие геометрически подобную проточную часть;
2) кинематически подобные (изогональные) режимы работы – имеют место в подобных насосах и выражаются в подобии скоростных полей.
Пусть насос I работает на определенном режиме, которому соответствует параллелограмм (треугольник) скоростей на выходе его колеса (I).
Предположим, что насос II подобен насосу I и работает на изогональном с ним режиме.
Все скорости в параллелограмме скоростей изменяются в одинаковое число раз, а углы лопатки и
Рисунок 8.1 – Треугольники скоростей
потока ![]() не меняются.
не меняются.
Из треугольников скоростей для насосов I и II следует:
![]() отсюда видим,
что
отсюда видим,
что ![]()
Тогда 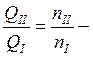 I-й
закон пропорциональности для турбомашин.
I-й
закон пропорциональности для турбомашин.
Из уравнения Эйлера теоретический
напор, развеваемый колесом насоса равен: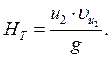
Из треугольников скоростей
следует, что ![]() и
и ![]()
Тогда действительный напор
насоса: ![]() где
где ![]() потери
напора в насосе.
потери
напора в насосе.
Для турбулентного режима
работы: ![]() где
где ![]() сопротивление
насоса.
сопротивление
насоса.
Для подобных насосов на
изогональных режимах можно считать ![]() и
и ![]()
![]() отсюда
видим, что
отсюда
видим, что ![]()
Тогда 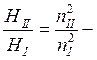 II-й
закон пропорциональности для турбомашин.
II-й
закон пропорциональности для турбомашин.
Мощность насоса: 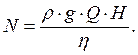
Для изогональных режимов работы насоса КПД ![]()
![]() отсюда
видим, что
отсюда
видим, что ![]() Тогда
Тогда 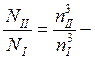 III-й закон пропорциональности для турбомашин.
III-й закон пропорциональности для турбомашин.
Рассмотрим пересчет
характеристики насоса с частоты вращения ![]() на
частоту вращения
на
частоту вращения ![]() причем
причем ![]()
Формулы пересчета берем из законов пропорциональности для турбомашин:
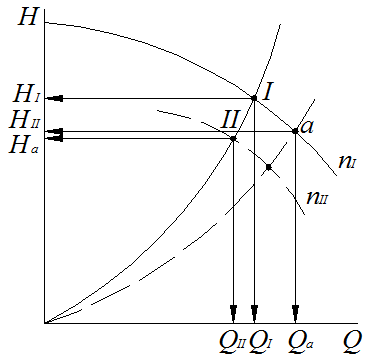
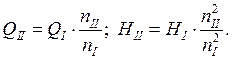
Задаваясь на ней т. I с
координатами ![]() получим по формулам пересчета
получим по формулам пересчета ![]() на характеристике насоса, которые
соответствуют частоте вращения
на характеристике насоса, которые
соответствуют частоте вращения ![]()
Найдем в координатах ![]() геометрическое место точек режимов
подобных тому режиму, который определяется точкой I.
геометрическое место точек режимов
подобных тому режиму, который определяется точкой I.
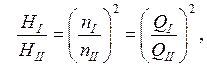 отсюда
отсюда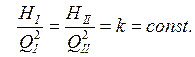
Кривая с уравнением ![]() называется
называется
Рисунок 8.2 – Напорно-расходная параболой подобных режимов.
характеристика
Точка I – своя парабола
при ![]() точка II – своя
точка II – своя
Пример: задана напорно-расходная
характеристика насоса с частотой вращения ![]() и
рабочая точка системы
и
рабочая точка системы ![]() Найти частоту вращения
Найти частоту вращения ![]() при которой характеристика насоса
пройдет через точку
при которой характеристика насоса
пройдет через точку ![]()
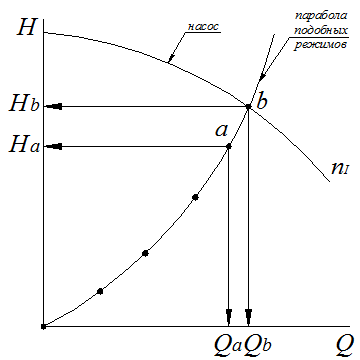 Решение:
Решение:
1) Проведем через точку ![]() параболу подобных режимов, найдя
параболу подобных режимов, найдя ![]() по формуле:
по формуле:
|
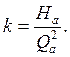
2) Парабола подобных режимов
пересечется с характеристикой насоса в точке ![]()
3) Частота вращения ![]() при которой характеристика насоса
пройдет через точку
при которой характеристика насоса
пройдет через точку ![]() определяется из I-го и II-го
законов пропорциональности для турбомашин:
определяется из I-го и II-го
законов пропорциональности для турбомашин:
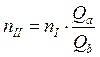 или
или
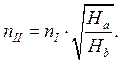
5. Работа насоса на простой трубопровод.
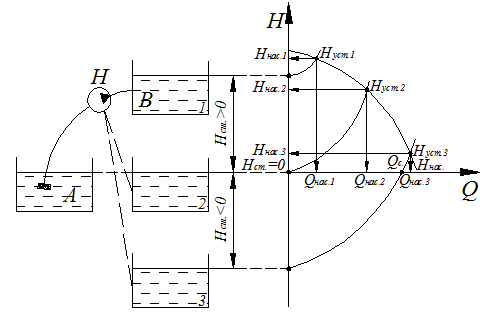
Пусть
насос![]() перекачивает жидкость из питателя
перекачивает жидкость из питателя ![]() в приемник
в приемник ![]() при
этом напорный трубопровод является простым. В работе насоса возможны три
случая:
при
этом напорный трубопровод является простым. В работе насоса возможны три
случая:![]()
![]() Начало координат выберем на уровне напоров
в баке
Начало координат выберем на уровне напоров
в баке ![]() В координатах
В координатах ![]() проводим характеристику насоса и
характеристику установки
проводим характеристику насоса и
характеристику установки 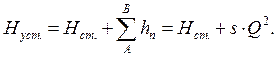
Рисунок 9.1 –
Схема работы насоса на простой Если баки![]() и
и![]() открыты в атмосферу,
открыты в атмосферу,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.