Расчет пути на прочность. Основные расчетные характеристики пути и подвижного состава, страница 5

II. Расчет пути на устойчивость.

2.1 Определение критической температурной силы.

Критическая температурная сила может определяться двумя способами: по методике Мищенко (энергетические уравнения) и по методике Першина (дифференциальные уравнения). В данном курсовом проекте для расчета критической температурной силы будем использовать методику Першина:

, где  – критическая сила, вызывающая выброс пути;

А – параметр, учитывающий тип рельса;

 – параметр, учитывающий план линии;

 – средний уклон начальной неровности (для прямой j = 2‰,                     для кривой j = 3‰);

 – коэффициент, зависящий от сопротивления балласта смещению шпалы ();

 – коэффициент, зависящий от эпюры шпал (для прямой , для кривой );

 – коэффициент, учитывающий степень затяжки болтов ();

Параметры А и μ определяются из табл.7 путем интерполяции.

Табл. 7

R, м	А при рельсах		μ при рельсах
	Р50	Р65	Р50	Р65
400 600 800 1000 Прямая	2380 2950 3320 3600 5170	2480 3150 3610 3830 5830	0,300 0,365 0,410 0,450 0,600	0,232 0,335 0,385 0,410 0,585

Критическая сила в прямой:

,

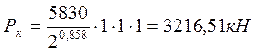Критическая сила в кривой:

.

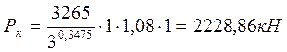Далее определим минимальную температурную силу, вызывающую выброс пути:

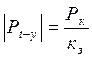, где к_з – коэффициент запаса (к_з = 1,5);

для прямого участка пути:

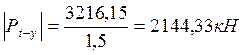, для кривого участка пути:

.

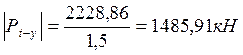Теперь можно определить допустимый интервал по устойчивости:

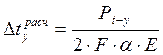, где F – площадь поперечного сечения рельса ();

α – коэффициент температурного расширения стали ();

Е – модуль упругости рельсовой стали ();

в прямом участке пути:

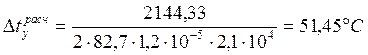, в кривом участке пути:

.

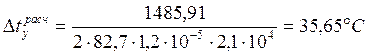Полученные значения сравниваем с о значениями, взятых с диаграммы:

Рис.8. Диаграмма допустимых повышений температуры рельсов Р65 бесстыкового пути по сравнению с температурой их закрепления  на железобетонных шпалах.

1 – 2000 шпал на 1 км, 2 – 1840 шпал на 1 км.

Из диаграммы: на прямой: , на кривой R=650м: .

Расчетные значения превышают диаграммные на 14%. Это превышение не столь велико и принимаем расчетные значения и .

Определим температурную силу, возникающую в рельсе при изменении температуры на 10, 15, 20 и 25°С:

, где α – коэффициент температурного расширения стали ();

Е – модуль упругости рельсовой стали ();

Δt – изменение температуры рельса по сравнению с температурой  закрепления;

F – площадь поперечного сечения рельса ();

,

,

,

.

III. Расчет бесстыкового пути .

3.1 Расчет бесстыкового пути на прочность.

В результате расчета бесстыкового пути на прочность мы определяем значения допустимых отклонений температур рельсов (сверх температуры закрепления). Для этого определяем напряжения сжатия в головке рельса для лета , так как в этом случае сжимающие изгибающие напряжения суммируются с сжимающими температурными; и растягивающие напряжения в подошве для зимы , когда растягивающие напряжения от изгиба в подошве суммируются с растягивающими температурными напряжениями.

Условие прочности:

,

, где  – кромочные напряжения в головке или подошве рельса;

 к_з – коэффициент запаса (к_з = 1,3);

 – температурные напряжения;

 – допускаемые напряжения;

α – коэффициент температурного расширения стали ();

Е – модуль упругости рельсовой стали ();

Δt – изменение температуры рельса по сравнению с температурой  закрепления;

Для термообработанных рельсов первого срока службы принимаем:

.

Для изменений температуры рельса на 10°С:

, на 15°С:

, на 20°С:

, на 25°С:

.

Кромочные напряжения в подошве рельса зимой берем из расчетов напряжений в элементах ВСП (п. 1.4):

наибольшее напряжение на прямой: , наибольшее напряжение в кривой: .

Напряжения в головке рельса определяются по формуле:

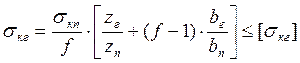, где  – напряжение в подошве рельса;

z_г, z_п – расстояние от горизонтальной оси до крайних волокон соответственно головки и подошвы рельса с учетом износа рельса (из табл. 1);

f – коэффициент, учитывающий влияние боковых и внутренно приложенных сил (из табл. 2);

b_г, b_п – ширина головки и подошвы рельса соответственно (из табл. 1);

для прямого участка:

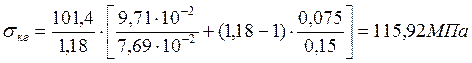, для кривого участка:

.

Дальше определяем допускаемые интервалы температур: