Математика \ Математическое моделирование систем и процессов

Методические указания и варианты индивидуальных заданий для студентов заочного факультета, страница 9


1/4	1	– 1/4	0	0	3	–
5/2	0	1/2	1	0	20	40
– 3/2	0	1/2*	0	1	4	8
13/4	0	3/4	0	0	-9
– 1/2	1	0	0	1/2	5	–
4*	0	0	1	–1	16	4
– 3	0	1	0	2	8	–
11/2	0	0	0	– 3/2	–15
0	1	0	1/8	3/8	7
1	0	0	1/4	– 1/4	4
0	0	1	3/4	11/4	20
0	0	0	–11/8	– 1/8	-37

Из последней таблицы мы получим оптимальное решение канонической задачи (25):

, , , , , , а следовательно функция принимает свое максимальное на множестве значение равное в точке с координатами ; .

6. Двойственная задача к искомой задаче будет иметь вид:

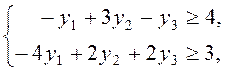
, или в матричной форме: , , с матрицами (24) и матрицей .

7. Из последней симплекс таблицы мы найдем значения двойственных переменных:

, ,

Подставим эти числа в ограничения двойственной задачи и целевую функцию:

, , .

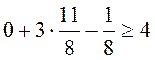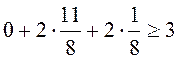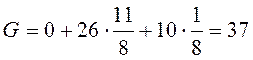Так как выполнены все условия теоремы двойственности, то найденное решение:

, , ,

будет оптимальным решением двойственной задачи.

Варианты заданий

1 ,

2 ,

3 ,

4 ,

5 ,

6 ,

7 ,

8 ,

9 ,

10 ,

11 ,

12 ,

13 ,

14 ,

15 ,

16 ,

17 ,

18 ,

19 ,

20 ,

21 ,

22 ,

23 ,

24 ,

25 ,

26 ,

27 ,

28 ,

29 ,

30 ,

31 ,

32 ,

Литература

Ашманов С.А. Линейное программирование, М., Наука, 1981, 340с.
Галанова З.С., Родин В.И., Ермошин А.А., Конова С.Ю. Линейное программмирование, ч.1, Петербургский государственный университет путей сообщения, 1996, 40 с.
Луценко М.М. Линейная алгебра. Учебное пособие. СПб: Петербургский государственный университет путей сообщения, 1999. – 121 с.

Учебное издание

ЛУЦЕНКО МИХАИЛ МИХАЙЛОВИЧ

Отпечатано в авторской редакции

Подписано в печать с оригинал макета – 6.04.2006

Формат 60х80 1/16. Бумага для множ. апп. Печать офсетная.

Усл.печ.л. Уч.-изд.л. Тираж

Заказ Цена

Петербургский государственный университет путей сообщения.

190031, СПб., Московский пр., 9.

1 2 3 4 5 6 7 8 9

Скачать файл