Методические указания и варианты индивидуальных заданий для студентов заочного факультета, страница 5

Таблица 5 порождает следующее базисное решение задачи:

, , , , .

Значение целевой функции будет . То есть на новом базисном плане оно меньше на 35 единиц, чем на первоначальном.

Найденное нами базисное решение не оптимально, так как в последней строке Таблицы 5 есть положительные элементы. Для нахождения следующего базисного плана выберем базисный столбец симплекс-таблицы 5. Так как в последней строке положительный элемент только один, то за такой столбец следует взять столбец .

Как и ранее вычислим отношения свободных членов к положительным элементам генерального столбца. У нас получатся следующие отношения: 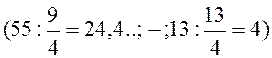. Наименьшим из этих отношений оказалось третье и, следовательно, генеральной строкой будет третья строка. Таким образом, генеральным элементом таблицы 5 будет число .

Выполним преобразование таблицы 5 и составим таблицу 6. Составление этой таблицы удобно начинать с последней строки, так как именно по ней определяется оптимальность получаемого решения. Так как все элементы последней строки оказались отрицательными, то порождаемое этой таблицей базисное решение

, , , ,

будет оптимальным, а минимальное значение целевой функции .

Построение допустимого плана с помощью искусственного базиса

Как мы уже отмечали, преобразования симплекс метода могут выполняться только с базисного допустимого решения. Однако поиск такого решения также довольно непрост. Формально мы должны перебирать базисные решения до тех пор пока мы не найдем неотрицательное или не покажем что таких не существует.

В этом параграфе мы покажем, как симплекс-методом можно найти базисное допустимое решение или доказать, что система ограничений канонической задачи несовместна.

Предположим, что в системе уравнений (12) значения свободных членов отрицательны. Умножим эти уравнения на –1 и составим новую систему уравнений:

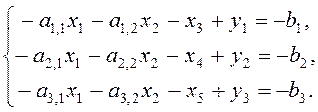                                   (14)

В этой системе искусственные переменные  можно взять за базисные, тогда все компоненты базисного решения  будет неотрицательны.

Составим новую задачу:

 при ограничениях (14) и .

Наименьшее возможное значение вспомогательной целевой функции  равно нулю и оно достигается только в том случае, когда значения всех переменных  равны нулю и они выведены из числа базисных. Таким образом, среди базисных переменных будут только иксы, а значит, был построен базисный допустимый план, и в дальнейшем переменные игреки можно не рассматривать.

Если же минимальное значение вспомогательной функции  положительно, то система (12) не имеет базисного решения с неотрицательными компонентами.

Пример 8. Решить следующую задачу линейного программирования симплекс методом.

                                                     (15)

при ограничениях

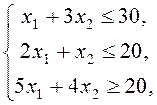
   .                                  (16)

Решение. Введем дополнительные переменные

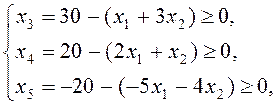
и перейдем к канонической задаче линейного программирования.