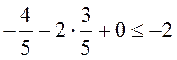 ,
, 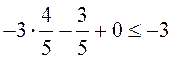 .
.
Следовательно, план ![]() является допустимым для задачи (15, 16). Вычислим
теперь значение целевой функции на этом плане. У нас получиться:
является допустимым для задачи (15, 16). Вычислим
теперь значение целевой функции на этом плане. У нас получиться:
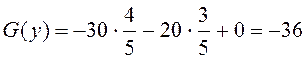 .
.
Это значение совпадает с сосчитанным ранее значением целевой функции прямой задачи. А поэтому приведенный нами план двойственной задачи (23) будет оптимальным.
Задача 4. Найти максимум линейной
функции ![]() , если переменные
, если переменные ![]() удовлетворяют
следующей системе ограничений:
удовлетворяют
следующей системе ограничений:
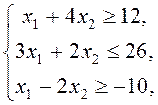
![]() .
.
В математических символах эта задача имеет следующий вид:
![]() ,
,
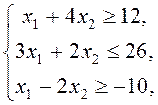
![]() .
.
1. Запишем эту задачу в матричной форме. Для этого умножим первое и третье неравенство системы на –1. У нас получиться следующая система неравенств:
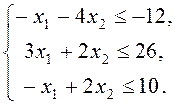
Следовательно, наша задача в матричной форме примет вид:
![]() ,
,
![]() ,
, ![]() , где
, где
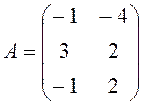 ;
;
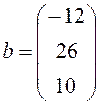 ;
; 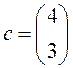 ;
; 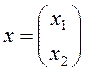 (24)
(24)
2. Для
построения канонической задачи введем дополнительные переменные ![]() и запишем систему ограничений задачи в
виде
и запишем систему ограничений задачи в
виде
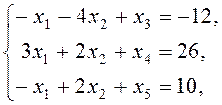
![]() .
.
Окончательно, каноническая задача линейного программирования для нашей задачи имеет вид:
![]() при ограничениях
при ограничениях
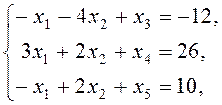
![]() .
(25)
.
(25)
![]()
![]()
|
|
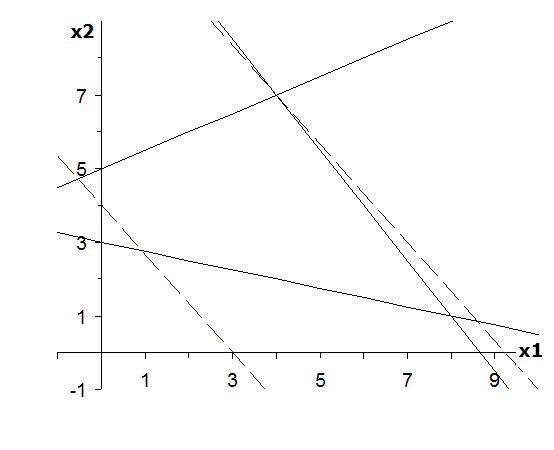 3. Для того чтобы решить начальную задачу геометрически,
построим прямые
3. Для того чтобы решить начальную задачу геометрически,
построим прямые и отметим стрелочками те полуплоскости, в которых выполняются соответствующие неравенства. Областью допустимых решений задачи оказался четырехугольник.
![]()
![]()
|
|
|
Функция ![]() принимает свое максимальное на множестве
принимает свое максимальное на множестве ![]() значение равное
значение равное ![]() в
точке с координатами
в
точке с координатами ![]() ;
; ![]() .
.
4. Если
за базисные переменные канонической задачи (25) взять переменные ![]() , то соответствующий базисный план будет
недопустим. Для построения начального плана введем искусственную переменную
, то соответствующий базисный план будет
недопустим. Для построения начального плана введем искусственную переменную ![]() и составим вспомогательную задачу.
и составим вспомогательную задачу.
![]() ,
,
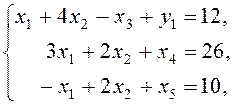
![]() .
.
Составим
симплекс-таблицу и применим симплекс метод. В таблицы включена также функция ![]() , а генеральные строки и столбцы таблиц
заштрихованы.
, а генеральные строки и столбцы таблиц
заштрихованы.
|
|
|
|
|
|
|
|
|
|
|
|
1 |
4* |
-1 |
0 |
0 |
1 |
12 |
12/4 |
|
|
3 |
2 |
0 |
1 |
0 |
0 |
26 |
– |
|
|
-1 |
2 |
0 |
0 |
1 |
0 |
10 |
10/2 |
|
|
4 |
3 |
0 |
0 |
0 |
0 |
0 |
|
|
|
1 |
4 |
-1 |
0 |
0 |
0 |
12 |
|
|
|
1/4 |
1 |
– 1/4 |
0 |
0 |
1/4 |
3 |
|
|
|
5/2 |
0 |
1/2 |
1 |
0 |
– 1/2 |
20 |
|
|
|
-3/2 |
0 |
1/2 |
0 |
1 |
– 1/2 |
4 |
|
|
|
13/4 |
0 |
3/4 |
0 |
0 |
– 3/4 |
-9 |
|
|
|
0 |
0 |
0 |
0 |
0 |
– 1 |
0 |
Из этой таблицы мы находим допустимый базисный план канонической задачи:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
5.
Исключим теперь из таблицы вспомогательную функцию ![]() , искусственную
переменную
, искусственную
переменную ![]() и решим полученную задачу
симплекс методом.
и решим полученную задачу
симплекс методом.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.