Методические указания и варианты индивидуальных заданий для студентов заочного факультета, страница 6

,                                                    (17)

при ограничениях

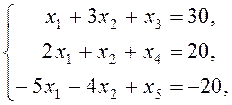                                               (18)

.

Если в этой задаче переменные  взять за базисные, а  за свободные, то базисным решением системы уравнений будет набор: , пятая компонента которого отрицательна. То есть это решение будет недопустимым. Следовательно, за базисные мы должны взять какие-то другие переменные.

Введем искусственную переменную  в третье уравнение:

и составим вспомогательную целевую функцию:

, в записи которой базисная  переменная  выражена через свободные. Составим вспомогательную задачу.

при ограничениях

.

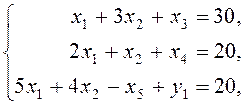
Для этой задачи составим симплекс-таблицу 7. В эту таблицу мы включили первоначальную целевую функцию , которая будет преобразовываться по тем же правилам, что и вся симплекс-таблица.

Таблица 7.                                                               Таблица 8.

За генеральный столбец в таблице 7 мы возьмем столбец . Отношения свободных членов к элементам этого столбца будут соответственно равны . Поэтому генеральный элемент будет в третьей строчке и равен 5. После преобразований у нас получиться таблица 8.

Переменная  вошла в число базисных вместо переменной , а минимальное значение вспомогательной функции  равно нулю. Следовательно, нами построено базисное допустимое решение канонической задачи (17, 18):

 , , , , .

Заметим, что значение целевой функции  на этом решение равно –8. Симплекс таблица для первоначальной задачи получается из таблицы 8 вычеркиванием столбца  и последней строки .  У нас получиться симплекс-таблица 9.

Таблица 9.                                                           Таблица 10.