Методические указания и варианты индивидуальных заданий для студентов заочного факультета, страница 4

·  Генеральный элемент таблицы помечается знаком *.

Составление новой симплекс таблицы.

·  Имена всех базисных переменных сохраняются за исключением имени генеральной строки. Оно заменяется именем переменной генерального столбца.

·  Элементы генеральной строки делятся на генеральный элемент, и полученные значения заносятся в новую таблицу. В частности, на месте генерального элемента записывается единица.

·  Остальные элементы генерального столбца заменяются нулями.

·  Для элемента  исходной таблицы находятся соответствующий ему элемент генеральной строки  и элемент  генерального столбца. На месте этого элемента в новой таблице пишется

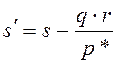,                                               (13)

где  – генеральный элемент.

Компактно это преобразование таблицы можно записать в виде формулы:

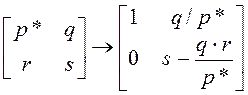
Пример 7. Решить следующую каноническую задачу линейного программирования симплекс-методом.

,                                         при ограничениях

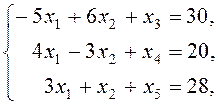
Решение. В этой задаче легко выделить базисные и свободные переменные. Полагая значения свободных переменных  нулю, найдем значение базисных переменных: , , . Полученное базисное решение  очевидно неотрицательно и, следовательно, допустимо. Составим теперь (базисную) симплекс-таблицу в первом столбце, которой указаны имена базисных переменных. (Таблица 3.)

Таблица 3.                                                                Таблица 4.

Эта таблица не порождает оптимальное базисное решение, так как в последней строке стоят два положительных числа. Возьмем одно из них, например 7. Следовательно, первый столбец будет генеральным. Найдем теперь отношения свободных членов к положительным элементам генерального столбца: 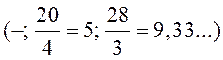. Наименьшее из этих отношений оказалось во второй строке. Пометим генеральный элемент символом *.

Переменную  введем вместо  в число базисных. На месте генерального элемента  запишем число 1, вместо остальных элементов генерального столбца запишем нули, все остальные элементы генеральной строки поделим на генеральный элемент, число 4. В результате мы получим таблицу 4.

Заполним клетку помеченную символом (·). Соответствующие элементы генеральной строки и столбца будут равны: , , поэтому в этой клетке следует написать 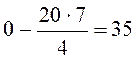 ( по формуле 13). В клетке, помеченной знаком (··), напишем 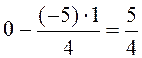. Аналогично заполняются оставшиеся клетки Таблицы 4. (Таблица 5.)

Таблица 5.                                                                Таблица 6.