Методические указания и варианты индивидуальных заданий для студентов заочного факультета, страница 7

В этой таблице выберем генеральный элемент и выполним преобразование таблицы. У нас получиться Таблица 10. В этой таблице значение целевой функции  равно –20, что меньше чем в таблице 9. Снова применим алгоритм симплекс метода. У нас получится Таблица 11.

Таблица 11.

Все элементы последней строки отрицательны. Следовательно эта таблица порождает оптимальное базисное решение задачи (17, 18). А именно,

, , , , .

При этом минимальное значение функции равно –36.

Минимальное значение функции  задачи (25, 16) равно также –36 и оно достигается в точке с координатами , .

Двойственная задача и теорема двойственности

Определение 9. Следующая задача называется двойственной к задаче (1,2).

Задача 3. Найти

,                                                                  (19)

, ,                                                                   (20)

где матрицы A, b,c определяются по формулам (3), а .

В развернутой форме эта стандартная задача линейного программирования может быть записана в следующем виде.

Задача 3’. Найти минимум линейной функции

,                                      

при ограничениях:

                                           

.

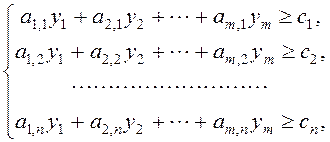
Задачи (1, 2) и (91, 92) называются взаимно двойственными задачами, а задача (1, 2)  по отношению к задаче (91, 92) называется прямой.

Пример 9. Составить двойственные задачи к следующим задачам.

a) , .

b) ,   .

Решение. a) Число переменных в двойственной задаче совпадает с числом ограничений прямой задачи и равно 3. Обозначим их через  Так как в прямой задаче требуется найти максимум, то знаки неравенств во всех ограничениях должны быть «». Коэффициенты целевой функции двойственной задачи совпадают со свободными частями неравенств, а правые части неравенств двойственной задачи совпадают с коэффициентами целевой функции прямой задачи. В итоге мы получаем следующую задачу линейного программирования.

,

.

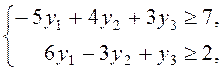
b) Прежде чем составить двойственную задачу следует прямую задачу преобразовать так, чтобы все неравенства в ней имели вид «». Для этого мы умножим первые два неравенства на –1. После этого мы уже сможем записать двойственную задачу.

,                               (21)

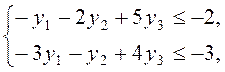
  .                               (22)

Для решения двойственной задачи можно применить те же методы решения, как и для прямой задачи: составление канонической задачи, поиск допустимого базисного плана, преобразование таблиц. Однако, всего этого можно избежать, если есть базисное решение прямой задачи. Базисное решение двойственной задачи можно взять из  строки для целевой функции прямой задачи. А для проверки оптимальности полученного решения можно воспользоваться теоремой двойственности.

Теорема двойственности. Пусть и допустимые решения задач и соответственно, тогда

1.  .

2.  Если , то   – оптимальные решения соответствующих задач.

Рассмотрим следующий пример решения двойственной задачи и проверки его по теореме двойственности.

Пример 10. Найти решение двойственной задачи к задаче примера 8 и проверить его по теореме двойственности.

Решение. Двойственной задачей к задаче (15, 16) будет задача (21, 22). Итоговой таблицей прямой задачи будет таблица 11. Меняя знаки у чисел стоящей в последней строчке, мы укажем значения переменных двойственной задачи.

, ,                                   (23)

Проверим теперь допустимость полученного решения. Для этого подставим их в неравенства системы (22). Мы получим