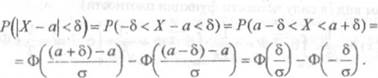Закон больших чисел. Некоторые распределения случайных величин (таблица)

Страницы работы

Содержание работы

причем функция Ф(х) табулирована и ее значения содержатся в уже встречавшемся нам приложении 2. Таким образом, с помощью этой таблицы мы ле:ко сможем вычислить всроњгнос•гь попадания Х в заданный интервал

ПРИМЕР

Пусть Хо — нормированная нормальная случайная величина. Найти

Решение

Р(-ОЈ «хо <0.3) - Ф(-О1) Ф(0.3) + 00398 0.1577.

Для нахождения значений функции Лапласа использовалась таблица из прил.

А как же нам справиться с ненормированным нормальным распределением Не можем же мы запастись таблицами значений на все случаи жизни, т.е. для всевозможных значений а и б. Ничего нс поделаешь, придётся вспомнить формулу замены переменной в определённом интеграле. Воспользуемся замено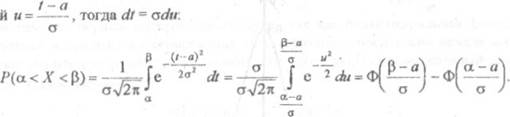й и:

ПРИМЕР

Пусть Х — нормально распределенная случайная величина с парамиграми а

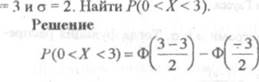= Ф(0) + = 0.4332.

Часто требуется вычислить вероятность того, что отклонение нормально распределённой случайной величины Х по абсолютному значению меньше заданного положительного числа 6, т.е. рох — Найдем эту вероятность, заменив неравенство эквивалентным ему двойным неравенством:

Поскольку Ф(х) нечетная функция, ф(бб), и окончательно име-

ем —

ПРИМЕР

Найти вероятность Того, что отклонение нормально распределённой слу-

чайно величины Х с парамејрами а и о не превышает утроенного среднеквадратического отклонения .

Решение Поскольку среднеквадратическое отклонение Х равно б, то искомая вероятность равна

р(х - • 2Ф(3) • 049865 = 0.9973.

Друмми словами, вероятность того, что абсолютная величина огклонения нормальной случайной величины превысит утроенное среднеквадратическое отклонение, очень мала, а именно равна I — 0.9973 = 00027.

Таксе событие является очень маловероятным, можно считать его практически невозможным. эк) означает, что на практике можно пренебречь этой вероятностью, которая составляет всего 0.27%. В этом состоит так называемое правило тлрёх сигм:

если случайная величина распределена нормально, то абсолютная величина её опплонения от математического ожиДания не превосхоДит утроенного среДнекваДртпического отклонения.

Подведем итоги этой главы, собрав все результаты в следующей таблице:

		ые аспределения
Название	Параметры		Закон еДеления
Биномиальноё	neN,			пр	npq
Пуассона

Пен е ьтшпщраспределения Название Параметры

Равномерное

Показа-лельнос 0, о, х 20.

Нормальнос	—е
Нормиро-	«х)	_ + ф(х)
ванное нор-		2

мальное

Таблица 2. Некоторые распределения случайных величин.

6. ЗАКОН БОЛЬШИХ ЧИСЕЛ

Как мы знаем, нельзя заранее с уверенностью предвидеть, какое из возможных значений прима случайная величина в результате испытания. Что же мы можем в таком случае сказать о поведении суммы достаточно большого числа случайных величин? Казалось бы, эта сумма есть величина в ещё большей мере непредсказуемая, чем каждая из случайных величин, но это не так. Оказывается, что при некоторых сравнительно широких условиях поведение достаточно большого числа случайных величин в совокупности почти утрачивает случайный характер и становится закономерным.

Эти необходимые условия и указываются в тео;хмах, носящих общее название закона больших чисел. К их числу относятся рассматриваемые ниже теоремы Чебышева и Бернулли. а также другие теоремы, которые мы рассматривать не будем. Заметим, что теорема Чебышева является наиболее общим законом больших чисел, а теорема Бернулли, наоборот, простейшим.

Доказательства этих теорем (которые мы по понятной причине в данном пособии опускаем) опираются на важное и интересное само по себе следующее

НЕРАВЕНСТВО ЧЕБЫШЕВА

Вероятность того, что отклонение случайной величины Х от её матепо абсолютной величине меньше положительного

числа е, не меньше, чем — рох -

Сформулированная ниже теорема Чебышева угвсржда«г, что если рассматривасгся достаточно большое число независимых случайных величин, имеющих ограниченные дисперсии, то почти достоверным можно считать событие, состоящее в лом, оаклонение среднего арифметического случайных величин ог среднего арифметического их математических ожиданий будет по абсолютной величине сколь угодно малым. Иными словами, среднее арифметическое достаточного большою числа случайных величин (при определенных условиях) есть всличина «почти» не случайная.

ТЕОРЕМА ЧЕБЫШЕВА

Если Хь Ха, Х„ — попарно независимые случайные величины, причём Дисперсии их равномерно ограничены, т.е. не превышают константы С, то

как бы мио ни бЬИ0 положительное число Е, вероятноапь неравенства Х, +Х2+...+Хп

будет как угоДло близка к еДиниче, если число случайных величин Достаточно велико.

Иными словами, в условиях теоремы lim

формулировке теоремы мы предполагали, что случайные величины имеют различные математические ожидания. На практике часто встречатся случай, когда математическое ожидание случайных величин одно и то же. Если дисперсии згих величин ограничены, то при применении к ним теоремы Чебышева мы получим следующее

СЛЕДСТВИЕ

Если Х, Хь Хя — попарно независимые случайные величины, имеющие одно и то же математическое ожиДание, равное а, и если Дисперсии эппјх ве-

45

„ч нчип равномерно ограничены, то как бы ни было мало число 00, имеет место слеДующее равепспио: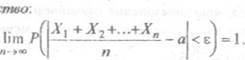

По определению предела и с учетом свойств вероятности •ло означает, что для любого ЕЯ.) наЙдегся такое Ы), зависящее от п и е, что

Давайте рассмотрим случайную величину Х = х ” +Х2+...4Х и, вос-

пользовавшись неравенством Чебышева, оценим значение б сверху. Пусть М(ХД — а, как в условиях следствия, а D(Xi) = д. Тогда АО“) — а и Ц.\') по

свойствам математического ожидания и дисперсии. Подставив зги значения в неравенство Чебышева, получив

(3)

В этом неравенстве можно также заменить случайные величины Ха, . Х„ на наблюдаемые при независимых испытаниях значения случайной величины с математическим ожиданием а и дисперсией д.