Решение
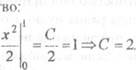 а) Функция должна удовлетворять
свойствам плотнос•м•. из первого свойслша значения нарамслра С должно быть нс
меньше нуля. Но зонно определить это значение поможет второе свойство:
а) Функция должна удовлетворять
свойствам плотнос•м•. из первого свойслша значения нарамслра С должно быть нс
меньше нуля. Но зонно определить это значение поможет второе свойство:
![]() •аким образом функция Лх) является плотностью распределения
при (2=2.
•аким образом функция Лх) является плотностью распределения
при (2=2.
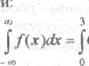 б) Аналогично, определим значение
параметра С исходя из второго свойства плотности:
б) Аналогично, определим значение
параметра С исходя из второго свойства плотности:
з ![]()
= fCx 2dx х![]()
3 З 9
в) Вычислим пределы Ах) на бесконечности:
![]() 2 тс. при С О эти пределы ненулевые и, следовательно, не
может являться плотностью распределения. Значение С 0 также не подходит,
поскольку в этом случае торос свойство заведомо не выполняется. Итак, ни при
каком значснии С функция Ах) не может являться плотностью распределения.
2 тс. при С О эти пределы ненулевые и, следовательно, не
может являться плотностью распределения. Значение С 0 также не подходит,
поскольку в этом случае торос свойство заведомо не выполняется. Итак, ни при
каком значснии С функция Ах) не может являться плотностью распределения. ![]()
г) Как и в предыдущем случае, функция Лх) не может являться плотностью распределения, поскольку при Сх 1 нарушатся свойство неотрицательносзи плотности.
Непрерывная случайная величина также может быть задана с помощью функции распределения, уже определенной нами в предыдущем разделе.
![]() Заметим, что если плотность распределения определена только
для непрерывной случайной величины, то функция распределения одинаково
определястся как для непрерывной, так и для дискретной случайной величины.
Заметим, что если плотность распределения определена только
для непрерывной случайной величины, то функция распределения одинаково
определястся как для непрерывной, так и для дискретной случайной величины.
Свойства функции распределения непрерывной случайной величины.
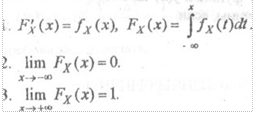
4. Функция FA(x) неубывающая.
Таким
образом, из первого свойства,![]()
![]() 34
34
![]()
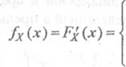
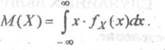
![]()
![]() ПРИМЕР
ПРИМЕР
Найти плотность распределения случайной величины Х, если
О, если х![]()
х, если х ![]()
1, если х Я.
Решение
По свойству функции распределения непрерывной случайной величины
(Х если х 4),
1, если х![]()
О, если х 1.
Итак, непрерывная случайная величина можег быть задана либо с помошью плотности распределения, либо с помощью функции распределения. Но, также как и для дискретной случайной величины, мы будем рассматривал чиеловые характеристики непрерывной случайной величины, а именно математичсское ожидание, дисперсию и среднеквадратическое отклонение.
Определение Математическим ожиДаиием непрерывной случайной величины Х называется
Определение. Дисперсией непрерывной случайной величины назынае1ся
Определение. СреДнекваДршпичеспьу отклонением непрерывной случайной
величины называется 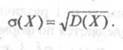
Если один из этих несобственных интегралов расходится, то говорят что соответствующая числовая характеристика для случайной величины Х не существует.
Замејим, что если определения математического ожидания для дискретной и непрерывной случайных величин различается, то определения дисперсии (через математическое ожидание) и среднеквадратического отклонения, в сущмости, совпадают. Друте дело, что формулы для их вычисления получаются разными для дискретых и непрерывных случайных величин.
Заметим также, что сели непрерывная случайная величина принимает значения только из некоторого интервала (a,b), то несобственные интетралы в тих определениях можно заменить на определенные с пределами а и Ь.
![]() 35
35
Также как и для дискретной случайной величины. для вычисления дисперсни непрерывной случайной величины можно получить более удобную формуЛУ:
ПРИМЕР
Найти математическое ожидание, дисперсию и среднеквадратическое отклонение для случайной величины, определенной в щкдыдушем примере.
Решение
2'
3'
1
5. НЕКОТОРЫЕ ЗАКОНЫ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНЫХ ВЕЛИЧИН.
Биномиальное распределение.
Вспомним схему последовательных испытаний Бернулли. Пусть проводится п независимых испытаний, в каждом из которых событие А может либо появиться, либо не появиться, причем вероятность появления события А равна р, а вероятность непоявления этот события в каждом испытании равна Рассмотрим в качестве случайной величины Х число успехов в мой серии из п испытаний. Тогда Х может принимать n•+l различных значений, от О до п. Соответствующие вероятности определяются по формуле Бернулли:
Торим. что случайная величина Х распределена по биномишљжшу закону. Запишем лот закон в виде таблицы:
Найдем матема•мчткое ожидание и дисперсию биномиального распределения. Для того введём п вспомогательных случайных величин Л, Х. которые отвечают за результат соответствующего испытания серии, т.е.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.