где ![]()
для дискретных случайных величин Хи У и
![]() , y)dxdy
, y)dxdy
для непрерывных случайных величин,
Корреляционный момент служит для характеристики связи между случайными величинами. В частности, для независимых случайных величин Х и У корреляционный момент Сху равен нулю.
По определению корреляционный момент имеет размерность, равную произведению размерностей величин Х и У. Это значит, что величина корреляционного момента зависит от единиц измерения случайных величин. Например, если при измерении величин Х и У в сантиметрах получилось С». 2 см2, то при измерении Х и У в миллиметрах получим Сху = 200 мм2. Такая зависимость корреляционного момента от единиц измерения затрудняет сравнение различных систем случайных величин. Чтобы устранить этот недостаток, вводится безразмерная характеристика rry связи между величинами Х и У, называемая коэффициентом корреляции:
![]()
Если случайные величины Х и У независимы, то r», = О.
Если же случайные величины Хи У связаны точной линейной зависимостью У = ах +
Ь, то rxy= l при а>О и Ъ. = — при а •z О. Вообще же справедливо двойное
неравенство —1 S rxyS![]()
Свойство независимости двух случайных величин Х и У в общем случае не равносильно их некоррелированности (т.е. равенству rn. = 0). Однако для нормально распределенных составляющих двумерной случайной величины это так.
ПРИМЕР 2
Закон распределения системы двух дискретных случайных величин (Х, Л задан следующей таблицей
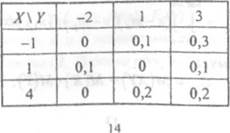
Найти:
![]() ) законы распределения случайных величин Х и У;
) законы распределения случайных величин Х и У;
2) условный закон распределения случайной величины Х при условии, что У = 1;
3) математические ожидания ИХ), Ц У) и центр рассеивания;
4) дисперсии D(X) и ДУЭ;
5) корреляционный момент Сду и коэффициент корреляции Ъ.
Решение
1. Сложив вероятности по строкам, получаем вероятности возможных значений случайной величины Х: = 0,4, p(l) = 0,2, р(4) = 0,4. Следовательно, закон распределения величины Х имеет следующий вид

Проверка: 0,4 + ![]() 1.
1.
Сложив вероятности по столбцам, получаем вероятности возможных значений случайной величины У: = 0,1, p(l) = 0,3, АЗ) = 0,6. Напишем закон распределения величины У
|
0,3 |
0,6 |
Проверка: (),l + 0,3 + 0,6 =![]()
2.
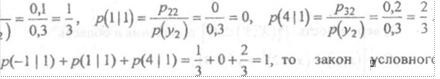 Найдем
условные вероятности для случайной величины Х при условии, что У = У-2 = 1:
p(-l f 1) = —Р12
Найдем
условные вероятности для случайной величины Х при условии, что У = У-2 = 1:
p(-l f 1) = —Р12
р(Ј'2)
Так как распределения (Х 1 У = 1) имеет следующую таблицу

15
З. Исходя из определения, вычисляем математические ожидания:
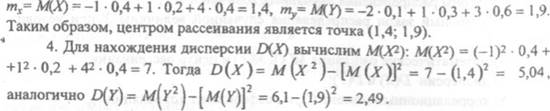
5. Составим таблицу системы чентривжанных случайных величин
х, У , где ![]() У=У-т = У -1,9
У=У-т = У -1,9
|
-2,4 |
о |
од |
0,3 |
|
2,6 |
о |
0,2 |
0,2 |
Вычислим корреляционный момент:
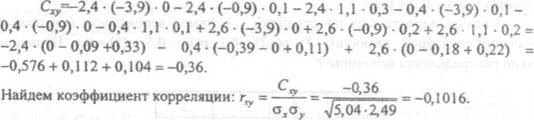 • (-3,9) • 0-2,4 • (-0,9) •
• (-3,9) • 0-2,4 • (-0,9) •
ПРИМЕР З
Система двух непрерывных случайных величин (Х, У) имеет равномерное распределение в области D = «х, у) — S х S 3, О S у S х + l} .
Найти:
![]() ) плотность распределения;
) плотность распределения;
2) вероятность Ч Х, У) с попадания в область
3) плотностиЛ(х) и Ку) распределения случайных величин Х и У, а также условные плотности и y(ylx);
4) функции и F20) распределения случайных величин Х и У;
5) математические ожидания М(Х), и центр рассеивания;
6) дисперсии и Ц У);
7) корреляционный момент Сл. и коэффициент корреляции
16
Решение
![]() 1. По
условию функция плотности имеет вид а, если —lSxS3 и 0SySx+l, О, если (х, у) Е
Д
1. По
условию функция плотности имеет вид а, если —lSxS3 и 0SySx+l, О, если (х, у) Е
Д
Для нахождения параметра а воспользуемся соотношением f(x, y)dy.dy = , где обл5сть интегрирования D изображена на рис. 7.
|
|
||||||||||||
рис. 7
Рис. 8
![]() Область D
ограничена слева и справа прямыми х = —1 и х = 3, а снизу и сверху — прямыми О
и У2(х) = х + 1. Переходя к повторному интегралу, имеем:
Область D
ограничена слева и справа прямыми х = —1 и х = 3, а снизу и сверху — прямыми О
и У2(х) = х + 1. Переходя к повторному интегралу, имеем:
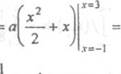
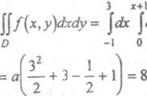 3
3
fady= гаурХ+1 Д = fa(x + l)dx =
=8а. Так как 8а = 1, ТО а з— и функция ПлОтнОсТи 8
имеет вид
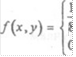
![]() —, если
—, если
О, если (х,у) Е).
17
2. Изобразим область G, которая представляет собой круг радиуса 2 с центром в точке (2, О) (см. рис. 8). Так как функция Ах, у) равна нулю вне

3. Найдем плотностиЛ(х) илу):
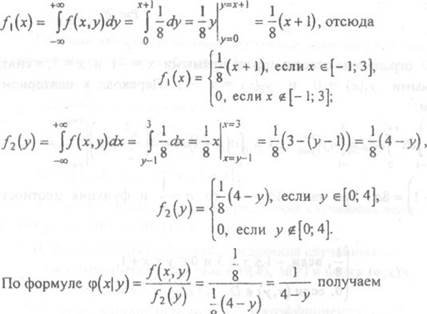 поэтому
поэтому
8
18 ![]()

Следовательно,
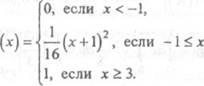
Для О S у S 4 аналогично получаем
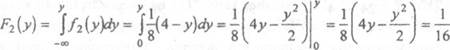 —(8у-у2
—(8у-у2![]()
Таким образом,
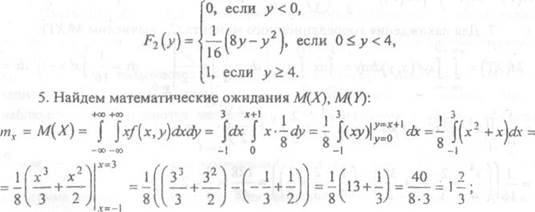
19
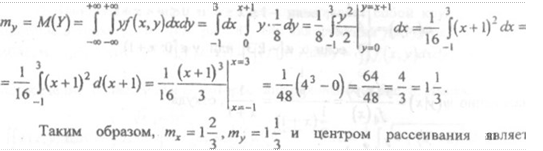
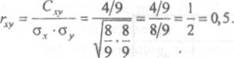 Тогда су = М(ХУ)- М(Х). м(у)
Тогда су = М(ХУ)- М(Х). м(у)
3 3 3 9 Найдем коэффициент корреляции:
точка 1— ,
![]() З.
ВЫБОРКА. СТАТИСТИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ.
З.
ВЫБОРКА. СТАТИСТИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ.
ПОЛИГОН И ГИСТОГРАММА.
 ВЫБОРОЧНЫЕ ХАРАКТЕРИСТИКИ
ВЫБОРОЧНЫЕ ХАРАКТЕРИСТИКИ
Задачей математической статистики является создание методов сбора и обработки статистических данных для получения научных и практических выводов. Более конкретно задача состоит в следующем.
Набор значений Щ, Ха, ..., может рассматриваться как система п независимых случайных величин
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.