![]()
![]()
![]()
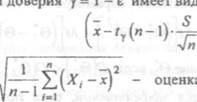
![]() указывают
интервал е- , накрывающий с заданной достаточно высокой вероятностью значение
параметра Э. Интервал (Э- называется
указывают
интервал е- , накрывающий с заданной достаточно высокой вероятностью значение
параметра Э. Интервал (Э- называется
Доверительным интервалом для неизвестного параметра Э с уровнен Доверия (т.е. с наДежностью) — Е (О Е к: 1), если вероятность того, что неизвестное значение е накрывается этим интервалом, равна 1—е:
Укажем формулы построения доверительных интервалов для параметров нормального распределения Фао, по выборке Щ, Х2, ...,Х„ объема п.
Если значение 62 известно, то доверительным интервалом параметра а с уровнем доверия у = — е будет интервал
где ![]() 5-2
, ф(х)
5-2
, ф(х) 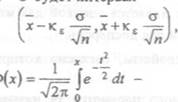 = функция нормального
= функция нормального
распределения, и к, находится из таблицы значений функции Ф(х) (см. таблицу в установочных лекциях для решения контрольной работы № 7).
Если значение 02 неизвестно, то доверительный интервал параметра а с уровнем доверия у = — Е имеет вид
, хну (п—![]()
где S = — —
оценка параметра о, ![]() значение
значение
функции по распределению Стьюдента с п — 1 степенью
свободы (см. прил.![]()
Доверительный
интервал для параметра б с уровнем доверия ![]() = 1 — Е равен
= 1 — Е равен
где — значение функции по распределению Х (см. прил. 2).
3. Критерии согласия. Приведем некоторые основные критерии согласованности статистического и теоретического законов распределения.
Пусть для данного статистического распределения найден близкий ему известный закон распределения.
Пирсон предложил следующий критерий согласованности статистического и теоретического распределений (Х -критерий). Сначала вводится величина
![]()
где — относительные частоты статистического распределения, а
р, ![]() вероятности, найденные из
теоретического закона распределения по следующему условию:
вероятности, найденные из
теоретического закона распределения по следующему условию:
если (4, 4) — область значений случайной величины Х, 4) < < ...< 4,
![]()
Затем, используя таблицу х2 -распределения (см. прил. З) при заданном достаточно малом значении Е > О (которое называется уровнем значимости), находим значение — 1). Если Х2 xt2 (k— 1), то делаем вывод, что теория плохо воспроизводит эксперимент. Если же Х2 < ХК (К — 1), то это означает, что гипотеза о принятом теоретическом распределении не противоречит опытным данным.
Определим критерий согласия Колмогорова-Смирнова. Пусть задано статистическое распределение

где — средние значения соответствующих интервалов случайной величины. Рассмотрим значение
где Fn(x) — эмпирическая функция распределения, Ах) — теоретическая функция распределения, а п — объем выборки. Найдем величину D„cn. Затем рассмотрим функцию
где ![]() е-2Ј
е-2Ј 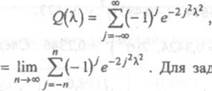 Для
заданного уровня значимости
Для
заданного уровня значимости
Е > О из таблицы значений функции Q(i) (см, прил. 4) найдем такое значение хк , при котором Q(Xt) = I — Е. Если 2 Х, , то гипотезу о согласованности эмпирического и теоретического распределений следует отвергнуть как неправдоподобную, а если DnG < Же, то гипотеза совместима с опытными данными.
31
ПРИМЕР 5
Даны О выборочных значений Х), Ха,![]()
|
—0 531 |
—0 4911 |
—0 516 |
о 025 |
—0 483 |
|
-1 254 |
-0 376 |
-0 582 |
-0,727 |
о 004 |
случайной величины Х, имеющей нормальный закон распределения с неизвестными параметрами а и 02 . Требуется:
1) вычислить точечные оценки а , с параметров а и 02 ,
принимая а = х, о2 = (о • (Х записать функцию плотности и найти р(х > ОД);
2) построить доверительные интервалы для параметров а и б с надежностью 0,95;
3) используя Х -критерий и критерий согласия Колмогорова-Смирнова с уровнем значимости Е = 0,05, оценить согласованность эмпирического и теоретического законов распределения, разбив интервал х — 1, х +1 на 5 равных частей.
Решение
![]() 2
2
![]() 1. Найдем значения а и о
1. Найдем значения а и о ![]()
![]()
![]() (-0,531
- 0,491 - 0,516 + 0,025 - 0,483 - 1,254 -
(-0,531
- 0,491 - 0,516 + 0,025 - 0,483 - 1,254 -
- 0,376 - 0,582 - 0,727 + 0,004) = -0,4931;
![]() (0,2820
+ 0,2411 + 0,2663 + 0,0006 + 0,2333 + 1,5725 +
(0,2820
+ 0,2411 + 0,2663 + 0,0006 + 0,2333 + 1,5725 +
+ о, 1414 + 0,3387 + 0,5285 + 0,0000) = 0,3604;
(6 2 )• = = 0,1173.
имеем = Дб = 0,3424, 2(6 2)• = 0,2346. Следовательно, функция плотности имеет вид
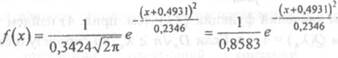
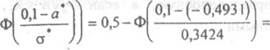 Найдем вероятность попадания случайной
величины в интервал (О. ; т): - 0,4931)
Найдем вероятность попадания случайной
величины в интервал (О. ; т): - 0,4931)
Р(х од) = 1- 0,1) =1- 0,5+
32
2. Найдем границы доверительного интервала параметра а Ж),
где
|
|
По прил. находим '195(9) = 2,31. Тогда
0,3610
—0,7568 ,
= -0,2294. мЛб Ji6
Таким образом, доверительный интервал параметра а с надежностью 0,95 равен (-0,7568; -0,2294).
Найдем теперь границы доверительного интервала для параметра о. По прил. 2 имеем 40,95, 10) = 0,65, Тогда
0,3610 • (1 -0,65) < 0,3610 • (1 + 0,65), 0,1264 < 0,5957.
Таким образом, доверительный интервал для б равен (ОД 264; 0,5957),
3. Оценим согласованность данного эмпирического и найденного теоретического распределения по х2 -критерию. Составим таблицу частот
|
(—1 ,4931 ; _1,0931) |
(-1,0931; -0,6931) |
(-0,6931; -0,2431) |
|
|
(-1,2931; 0,1069) |
(0,1069; 0,5069) |
||
|
2 |
и таблицу относительных частот для середин интервалов
|
х |
-1 ,2931 |
—0,8931 |
—0,4931 |
—0,0931 |
0,3069 |
|
од |
0,6 |
0,2 |
Вычислим вероятности ) = 0,5+ 0,3424
33
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.