Доверительный интервал для неизвестного параметра. Формулы построения доверительных интервалов, страница 2

од	0,0401	0,0599	0,0036	0,0895
	0,2409		0,0199	0,0824
	0,4380	0,1620	0,0262	0,0599
0,2	0,2409	—0,0409	0,0017	0,0069
	0,0401	-0,0401	0,0016	0,0401

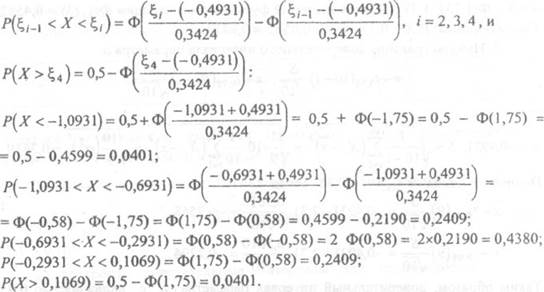
контроль: 0,0401 + 0,2409 + 0,4380 + 0,2409 + 0,0401 = 1.

2

Составим расчетную таблицу для вычисления значения Х

0,2788

тогда= 10 х 0,2788 2,788. По приложению 3 найдем

Х² = 2,788 < 9,49 = Й05(4), гипотеза о принятом

теоретическом распределении не противоречит опытным данным.

Выполним проверку согласованности распределений по критерию согласия Колмогорова-Смирнова.

Составим расчетную таблицу для вычисления значения х- 0,4931)

[АО = F(x), где ах) =                      = 0,5 +            0,3424

34

х
-1,2931		0,0100	0,0900
-0,8931	0,2	0,1210	0,0790
	0,8	0,5000	0,3000
-0,093		0,8790	0,2110
0,3069		0,9900	0,0100

Из таблицы находим максимальное значение: До = 0,3, откуда = 0,9487. Из прил. 4 найдем значение ха05, при котором Q(XQOS) = 1 — 0,05 = 0,95: = = 1,358. так как -0,9487 1,358 = хам, то гипотеза о нормальном распределении с параметрами а• = —0,4931 и = 0,3424 совместима с опытными данными.

5. ЭЛЕМЕНТЫ ТЕОРИИ КОРРЕЛЯЦИИ

Во многих задачах требуется установить и оценить зависимость данной случайной величины от других случайных величин. Две случайные величины Х и У могут быть связаны либо функциональной зависимостью (т.е. У = ЛАЭ или Х = Л Л), либо статистической зависимостью (при которой изменение одной из величин влечет изменение распределения другой), либо быть независимыми.

Статистическая зависимость случайных величин Х и У называется корреляционной, если при изменении одной из величин изменяется среднее значение другой.

Примером корреляционной, но не функциональной зависимости является количество поступающих товаров Х и их удельная стоимость У. При увеличении количества товаров их удельная стоимость не уменьшается как функция от Х . Однако средняя удельная стоимость снижается при росте количества товаров Х, т.е. У и Х связаны корреляционной зависимостью.

Уточним понятие корреляционной зависимости. Пусть (Х, УЭ — система двух случайных величин. Зафиксируем некоторое значение х случайной величины Х. При Х = х случайная величина У может принять любое значение из некоторого множества, причем заранее неизвестно, какое именно. Среднее значение этого множества ух называется математическим ожиданием случайной величины У, вычисленным при условии, что Х = х. Функциональная зависимость

35

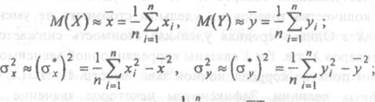
У, =Лх)            (1) называется корреляционной зависимостью У от Х. При этом уравнение (1 ) называется уравнением регрессии У на Х, функция Ах) — регрессией У на Х, а ее график — линией регрессии У на Х. Если значения ух остаются неизменными, говорят, что корреляционная зависимость случайной величины У от Х отсутствует.

Аналогично определяется корреляционная зависимость ху = ФО), регрессия Х на У и линия регрессии Х на У.

 Существуют две основные задачи теории корреляции. Первая заДача теории корреляции — установить форму корреляционной связи, т.е. вид функции регрессии (линейная, квадратичная, показательная и т.д.). Если обе функции Лх) и ФО) линейны, то корреляция называется линейной; в противном случае — нелинейной. Очевидно, при линейной корреляции обе линии регрессии являются прямыми.

Вторая заДача коррелячии — оценить тесноту (силу) корреляционной связи. Теснота корреляционной зависимости У от Х оценивается по величине рассеяния значений У вокруг условного среднего . Большое рассеяние свидетельствует о слабой зависимости У от Х либо об отсутствии зависимости. Малое рассеяние указывает на большую зависимость У от Х, возможно, даже функциональную.

Аналогично по величине рассеяния значений Х вокруг ху оценивается теснота корреляционной связи Хот У.

Пусть в результате п испытаний для системы случайных величин (Х, Ю получено п точек (х, , у), (ха, уа), (ха, уп) (среди этих точек могут быть и совпадающие). Вычислим коэффициент корреляции системы (Х, У), заменив математические ожидания ИХ) и Ц У) средними арифметическими значений соответствующих случайных величин. На основании закона больших чисел имеем:

С» „С; = -Ех,у - ХУ.

Отсюда можно найти выборочный коэффициент корреляции по формуле

36

Если 23, то связь между случайными величинами Х и У достаточно вероятна. Если связь между Х и У установлена, то линейное приближение функции ух дается формулой линейной регрессии

х— х , т.е. ух = ах+Ь.

Аналогично линейное приближение функции ху дается формулой линейной регрессии

                        ху    у— у, т.е. xy =cy+d.

Вывод данных формул основан на методе наименьших квадратов.

Выборочный коэффициент корреляции характеризует тесноту линейной связи между количественными признаками в выборке: чем ближе           единице, тем связь сильнее, чем ближе к нулю, тем связь слабее.

Для нахождения выборочных коэффициентов удобно пользоваться корреляционной таблицей

		У2
	nml	пт2

где Ч, ...,xm — все выборочные значения для случайной величины Х, И, ...,УА — все выборочные значения для случайной величины У, по — число повторений пары (Ч, у), пл, = — число повторений значения х, в парах,

У] =     — число повторений значения уј в парах.

ПРИМЕР 6

По данным корреляционной таблицы

37