Математика \ Высшая математика

Некоторые законы распределения случайных величин. Биномиальное распределение. Показательное распределение, страница 2


36

О, если в i - том испытании событие А не наступило,

1, если в - том испытшми событие А наступило.

Очевидно, что зги вспомогательные случайные величины независимы и распределены одинаково, принимая значение с вероятностью р и значение О с веротгпос•гыо q. Кроме того, Х = Xl + Хп.

0.q=p,

Таким образом, используя свойства математического ожидания и дисперсии, получим:

                    М(Х) = Д4(Х' + +                              +              = р + + р = пр,

Заметим, что если пр — целое, то это есть наиверотгнейшее число успехов в серии испытаний, что согласу«гся с вероятностным смыслом математического

Распределение Пуассона.

Случайная • величина Х, распределенная по закону Пуассона, принимает

натуральные значения О, 1, 2,       ..., причём Р(Х = К) =

К! Найдем М(Х) и D(X).

                                                 ike-x                        = ie -i

К!

Но последняя сумма есть ни что иное, как разложение экспоненты ех в ряд Тейлора при х = Х. Таким образом М(Х) = . вспомним, что АХ) = мф) - Найдем МС):

К!

(К -l)ik

      Таким образом,                                                                Х.

37

Равномерное распределение.

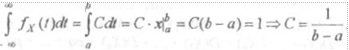
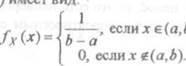
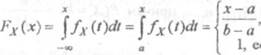
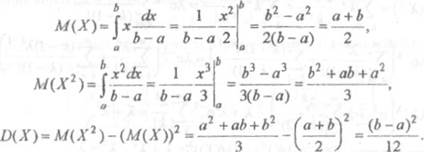
•оворят. что случайная величина Х распределена равномерно на шт•.рвале (а, Ь), сели плотносгь сё распрелслсния имеет вид:

С, если х

О, если х Е (а, Ь).

Исходя из свойств плотности распределения, параметр С не может приниМаи. произвольное значение, поскольку f_ = I . Найдем это значение:

Таким образом. Плотность случайной величины Х, равномерно распределенной на интервале (а,Ь) имеет ВИЛ:

Найдем функцию распределения Х. Очевидно, что при «а FA{x) О. А при

если х к: Ь, 1, если х) Ь.

О, если х S а,

        Итак, Fx (х) =            , если х

1, если х 2 Ь.

Найдем математическое ожидание и дисперсию Х.

Таким образом, дисперсия равномерного распределения зависит только от длины интервала (a,b), и нс зависит от расположения этого интервала, что демонстрируег четвертое свойство дисперсии, гласящее, что значение дисперсии

38


не зависш (УГ сдВит. А шуг математическое ожидание, наоборот, зависит только от расположения середины этого интервала, и не зависит от его длины.

11оказательное (экспоненциальное) распределение.

'оворим. что случайная величина распределена по показательному (или экспоненчиааьнаму) закону, если функция плотности ее распределения имеег

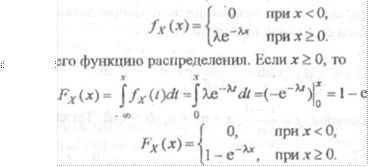              , т.е.

Таким образом, вероягность попадания показательно распределённой случайной величины Х в заданный интервал В) составляет (при 00)

ПРИМЕР

Непрерывная случайная величина Х распределена по показательному за-

кону:

при х при х 20.

         Найт ЦО.4            1).

Решение

Параметром Р(0.4 «Х

Найдем математическое ожидание и дисперсию показательного закона распределения .

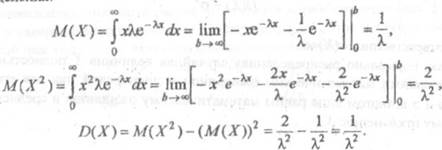
39

По наиболех: важное значение имеет следующее Нормальное распределение.

] •оворят, чзо случайная величина Х распределена по нормальному закону, если плотность её распределения 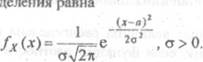равна

Заметим. что нормальное распределение определя€'№я двумя парамеарами - а и о, смысл которых мы поймём чуть позднее. А сейчас давайте вычислим 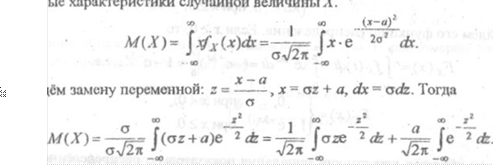числовые характеристики случайной величины Х.

Заметим, что первый интеграл равен нулю, так как подынтегральная функция нечётная, а пределы интегрирования симметричны относительно • начала координат. А интеграл во втором слагаемом — эзо интеграл Пуассона, который равен фп . Таким образом  лих) = о +2— . Г

Найдём теперь дисперсию D(X), зная, что М(Х) — а и воспользовавшись точно такой же заменой переменной:

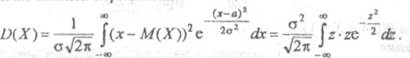
Предлатем читателю самостоятельно проинтегрировать последнее выражениепо частям (и —z, dv=e 2 ф) и убедиться, что

62.

Соответственно,


Итак, нормально распределенная случайная величина Х полностью определяася своими математическим ожиданием и дисперсией, так как его параметры а и о в чистом виде равны математическому ожиданию и среднеквадратмческому ктгклонению Х.

40

Дартлы.м нормальным.

— — нормированная нормальная случайная величина.

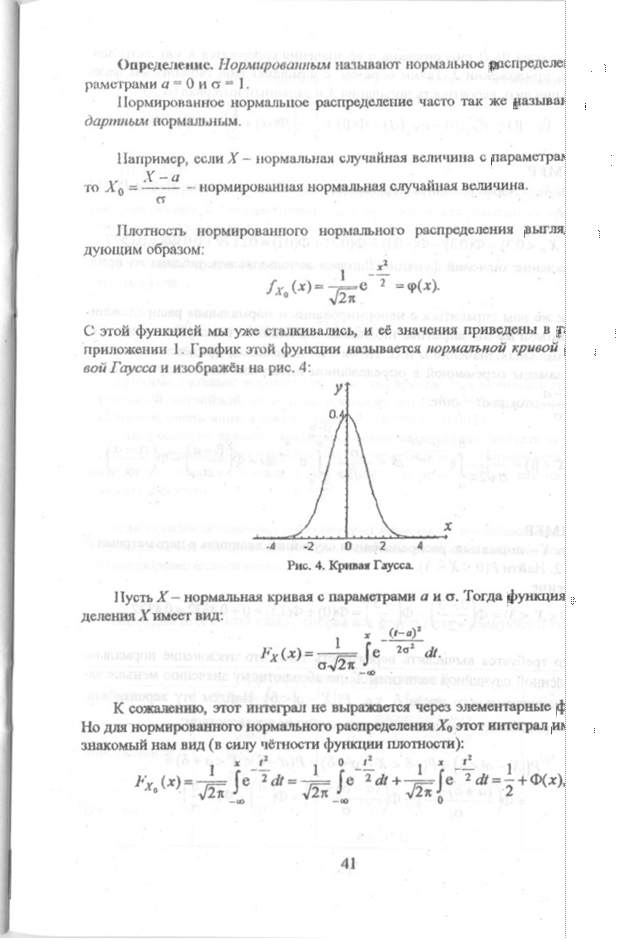
вой Гаусса и изображён на рис. 4:

х Рис. 4. Кривая Гаусса.

И.

знакомый нам вид (в силу четности функции шютносм):

41

Скачать файл