Установочные лекции по высшей математике. Контрольная работа. Двойные интегралы Системы случайных величин Элементы математической статистики

удк 51(07)

У797

В установочных лекциях, состоящих из восьми частей, приводится основной теоретический материал и решение типовых задач контрольных работ по высшей математике, предлагаемых студентам-заочникам экономических и пищевых специальностей на и ll курсах. Не заменяя подробных изложений курса высшей математики, изучение которых необходимо для подготовки к сдаче экзаменов, пособия позволяют выполнить контрольные работы. Правила оформления контрольных работ описаны в первой части.

Составители:

ИЯ. Глазычев, А.М. Ивлева, Л.В. Ковалевская, ЕВ. Овчинникова,

А.Г Пинус, КН. Пономарев, СВ. СуДоплатов, ИД. Черных,

А.В. ЧехонаДских, ВГ. Шихова

Рецензент д-р физ.-мат. наук, проф.

Работа подготовлена на кафедре алгебры и математической логики

С) Новосибирский государственный технический университет, 2002, 2008

1. ДВОЙНЫЕ ИНТЕГРАЛЫ

Пусть D — область в плоскости 0', отраниченная замкнутой линией L и включающая в себя эту линию. Рассмотрим функциюј(х, у), определенную в Ъ). Разобьем область D на п элементарных областей, имеющих соответственно площади •&Sl,  и диаметры Ц, 4, ...,dn (Диаметром области называется наибольшее из расстояний между двумя точками из этой области). Выберем в каждой элементарной области точку М к (Ц, , и рассмотрим выражение

Полученное 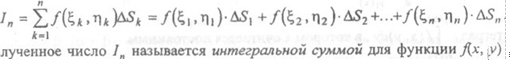число области D

Если при тах d, О существует конечный предел

интегральных сумм 1п, не зависящий от способа разбиения D на элементарные области и от выбора точек Мк в этих областях, то число называется двойным интегралом от функции Ах, у) в области D и имеет следующее обозначение:

Если Лх, у) > О в области D, то двойной интеграл  равен

объему цилиндрического тела, ограниченного сверху поверхностью = Их. у), сбоку — цилиндрическими поверхностями с образующими . параллельными оси (Е, а снизу — областью D в плоскости хОу. В частности, если Ах, у) Е 1, то двойной интеграл от функции Лх,у) в области D равен площади S области О. S = ffddy.

Отметим основные свойства двойного интеграла:

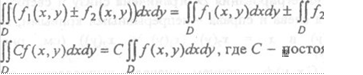           1.                                                                                    (х, y)dxdy .

2.

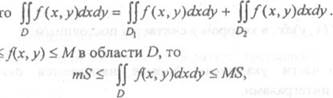3. Если область интегрирования D состоит из двух непересекающихся частей Dl и д, то

4, Если т

з

где S — площадь области Д т и М — соответственно наименьшее и наибольшее значения функции Лх, у) в области D

При практических вычислениях двойных интегралов пользуются следующими основными правилами:

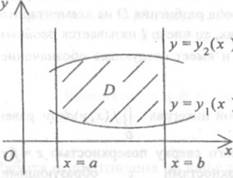
А. Если область интегрирования D ограничена слева и справа прямыми х = а и х = Ь (а < Ь), а снизу и сверху — непрерывными кривыми, заданными функциями у их) S У2(х)) (см. рис. 1), то

причем сначала вычисляется внутрен ни й

интеграл ff(x,            , в котором х считается постоянным.

)

)

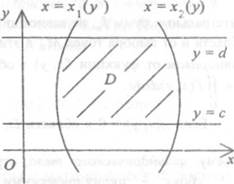
рис.

рис. 2

Б. Если область интегрирования D ограничена снизу и сверху прямыми у = с и у = d (с < d), а слева и справа — непрерывными кривыми, заданными функциями х = хо) и х = хо) (хо) S хо) (см. рис. 2), то d 12 (у) причем сначала вычисляется внутренний

интеграл                            в котором у считается постоянным.

Правые части указанных формул называются Двукратными (или повторными) интегралами.

4

В. Для вычисления интеграла по более сложной области D производится разбиение этой области на части, удовлетворяющие условиям пунктов А и Б, находятся интегралы по этим частям и результаты складываются на основании свойства 3 „

При переходе от првмоугольных декартовых координат х, у к полярным координатам r, ф, связанным с прямоугольными координатами соотношениями х = rcosp, у = rsincp, происходит преобразование двойного инте№ала по следующей формуле:

                                    =         cosp,r sinq*drdQ.

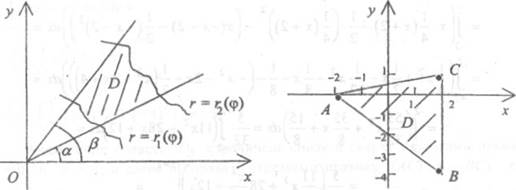
Если область интегрирования D ограничена двумя лучами

= а, ф = [3 (ц Р), ВЫхОдЯЩИМИ из полюса, и двумя кривыми, заданными функциями r = пф) и r = пф) (см. рис. 3), то двойной интеграл fff(r  вычисляется с помощью повторного интеграла по

формуле

cosp,r sinp)rdr.

                                       Рис, 3                                                                              Рис. 4

ПРИМЕР

Вычислить двойные интегралы:

Jf(x— y)dxdy, если область D образует треугольник с вершинами

0), в(2, -4), ср, 1).

5

ff6Pdxdy, если область D определена неравенствами

х ² + у? S —4х и у S —х.

Решение

1. Изобразим область D (см. рис. 4). Найдем уравнения сторон треугольника АВС как прямых, проходящих через две данные точки:

Область интегрирования D ограничена слева и справа прямыми х = —2 и х = 2, а снизу и сверху — отрезками прямых (АВ) и (АС), т.е.

= —х —2 и У2(х) = —(х +2). Переходя к повторному интегралу, получаем          

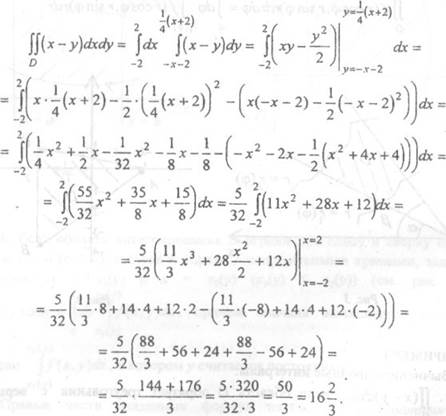
Задача может быть решена и переходом к повторному интегралу. в котором интегрирование ведется сначала по переменной х, а затем по

переменной у Разобьем треугольник АВС на два треугольника АВМ и АСМ,

общие стороны которых лежат на горизонтальной прямой, содержащей вершину А (см. рис. 5). Так как УА = О, то горизонтальная прямая имеет уравнение у = О. Пусть Dl — область, ограниченная треугольником АВМ, Г-)2 — область, ограниченная треугольником АСМ Найдем двойные интегралы от данной функции Лх, у) = х —у в указанных областях. Область ограничена снизу и сверху отрезками прямых у = — 4 и у = О, а слева и справа — отрезками прямых (АВ) и (ВС), т.е. у = —х—2и х 2, или х = — у— 2 и х = 2. Тогда

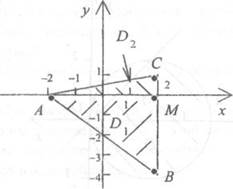
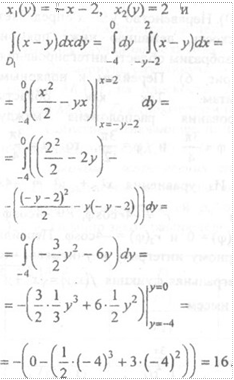                                       Рис 5

Аналогично область D2 ограничена снизу и сверху отрезками прямых у = О и у = 1, а слева и справа — отрезками прямых (АС) и (ВС), т.е.

у 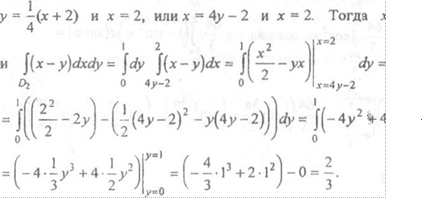= —(х+2) и х = 2, илих =4у—2 и х = 2. Тогда ЧЭ) = 4х—2,