Системы случайных величин. Средние квадратичные отклонения случайных величин по формулам

Окончательно получаем

                                                             — yprdy =        = 16?.

3

Отметим, что второй способ оказался сложнее, поскольку пришлось область D разбить на две части и вычислять два повторных интеграла.

-4	2

2. Так как х ² + у² S —4х    х ^а +4х+4+у ² S 4 (х+2)² + у² S 2 ² , то каждое из этих неравенств по формуле (х — хо)² + (у— уо)² S R² определяет круг радиуса R = 2 с центром в точке       О). Неравенство у S —.х определяет полуплоскость, лежащую ниже прямой у = —х. Изобразим область интегрирования D (см. рис. б). Перейдем к полярным координатам.           Так         как             область интегрирования расположена между Зл лучами ф = —        то ц = —

                                                                                      4                    2'                    4

                                                               р =                  Из уравнения х: + уп = —4х

находим = —4rcostp,         —4costp. Тогда О и «р) = —4сомр. Перейдя к повторному интегралу и учитывая, что подынтегральная функция Лх,у) =

                          рис. б                            равна r, имеем

9

8

2. СИСТЕМЫ СЛУЧАЙНЫХ ВЕЛИЧИН

Часто результат опыта описывается несколькими случайными величинами: Щ, Ха, Ха. В этом случае говорят, что указанные случайные величины образуют п-мерную случайную величину. или систему (Щ, Х1, ..., Х.).

Рассмотрим примеры систем случайных величин.

1.  Если станок штампует плитки, у которых контролируемыми размерами является длина Х, ширина У и высота 7., то получается трехмерная случайная величина (Х, У, О.

2.  При рассмотрении цены Х и спроса У на данные изделия имеет место двумерная случайная величина (Х, У).

Двумерную случайную величину (Х, У) можно изобразить случайной точкой М(Х, У) на плоскости, а трехмерную величину (Х, У, — случайной точкой ИХ, У, 7) в трехмерном пространстве.

Событие, означающее попадание случайной точки (Х, в область Д обозначается через (Х, У) с D.

Законом распределения системы двух Дискретных случайных величин (Х, У) называется множество всевозможных значений (х„уј) этой системы с указанием вероятностей ро одновременных выполнений равенств Х = х, и

У = уј. Обычно закон распределения задают в виде таблицы

		п
		P12		Р1п
		Рт2		Ртп

где х, < ха < <хт, у, уа ... < При этом сумма вероятностей Ьй строки равна вероятности наступления события Х = х,

сумма вероятностей ј-го столби равна вероятности наступления события

                                            = у) + + ртј,

а сумма всех вероятностей таблицы равна единице

9

Таким образом, закон распределения случайной величины Х имеет таблицу распределения

р	p(Xl)
где Ах) = +рп + + таблицу распределения		а закон распределения случайной величины У —
	pOl)	р(п)		рол)

где Ду)                     + + ртј.

Предположим, что в результате испытания величина У приняла значение

У = у. При этом величина Х примет одно из своих значений из множества Х = , х2 ,хп} . Обозначим через р(хлуј) условную вероятность того, что Х

примет значение х, при условии, что У =

Совокупность условных вероятностей p(xmlyj),

вычисленных в предположении, что событие У = у, уже наступило, называется условнььм распреДелением случайной величины Х при У = У).

Аналогично определяется условное распределение случайной величины У при Х = Xi.

При вычислении условных вероятностей пользуются соотношениями

Отметим, что сумма вероятностей

                р(уј)                 p(Xi )

условного распределения равна единице

Закон распределения системы двух непрерывных случайных величин (Х, У) задается с помощью функции плотности вероятности (или плотности распреДеления) Лх, у).

Вероятность попадания случайной величины (Х, У) в область D определяется следующим соотношением:

Функции 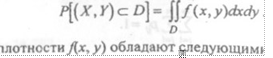свойствами:

10

1.

          2.                                                               где двойной несобственный интеграл

рассматривается как предел двойных интегралов по областям, расширяющимся в пределе до всей плоскости х(ђ.'.

Если все случайные точки принадлежат ограниченной области Д то условие 2 означает, что = 1.

Используя плотность Лх, у), находим плотности Л(х) и ЛО) распределений случайных величин Х и У

Функцией распреДеления двумерной случайной величины (Х, У) называется функция Ах, у), определяющая для каждой пары чисел х, у вероятность того, что Х примет значение, меньшее х, и У примет значение, меньшее у,

Перечислим основные свойства функции распределения.

1 . О  для любых х и у

2. ах, у) есть неубывающая функция по каждому аргументу, т.е.

F(X2, у) если х2 >

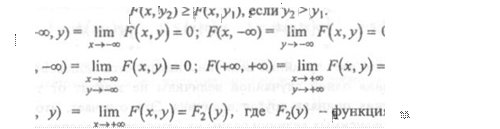О;

1;

случайной величины У;
ах. +Ф) = lim	где F1(x) — функция распределения

случайной величины Х.

предел Последнее отношения свойство вероятности означает, что попадания функцию случайной Лх, у) можно точки рассматривать в прямоугольниккак     входящих Математические в систему (Х, У), ожиДания определяются дискретных по формулам:случайных величин Х и У,

со сторонами и Лу к площади этого прямоугольника, когда обе стороны прямоугольника стремятся к нулю.

           Пусть (Х, У) — непрерывная двумерная случайная величина. Функция        а математические ожидания непрерывных случайных величин Х и У — по

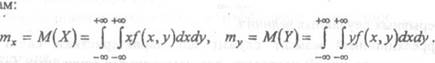(p(xly) =             называется условной плотностью случайной величины Х при                   формулам:

данном значении У = у. Отметим, что функция дает распределение случайной величины