Закон больших чисел. Некоторые распределения случайных величин (таблица), страница 2

Итак, сущность теоремы Чебышева такова: среДнее арифметическое Достаточно большого числа независимых случайных величин (дисперсии которых равномерно ограничены) утрачивает характер случайной величины.

Вспомним теперь схему испытаний Бернулли. Пусть производится п независимых испытаний, в каждом из которых верожтность появления события А равна р. Пусть в этой серии испытаний ровно т раз появилось событие А, т.е. т — случайная величина. распределенная по закону Бернулли. Можно предвидеть, какова будет примерно относительная частота появлений события? Положительный ответ на этот вопрос даёт следующая

ТЕОРЕМА БЕРНУЛЛИ

Если в кажДом из п незавиаьиьи испытаний вероятность р пояатения события А постоянна, то как угодно близка к еДинице вероятность того, чпю отклонение относительной частоты от вероятности р по абсолютной вешчине будет сколь угоДно малым. если число испыпитий Достаточно везико:

1im

46

Заме мм, '•гго из теоремы Бернулли не вытекает равенство lim -

теореме речь идет лишь о вероятности лого, •гго при достаточно большом числ: испьп•аний относительная часгога будет как угодно мало отличаться от постоянной вероятности появления события в каждом испытании. Именно из этого факта вытекает эквивалентность классического и статистического определений вероятност, но мы по понятным причинам не будем того строго доказывать — поверьте на слово.

Для ситуации, описанной в теореме Бернулли, тоже можно получить оценку, аналогичную (3 Она

                                                                   .                                      (4)

ПРИМЕР 1

Симметричную монету подбросили 1200 раз. Оценить снизу вероялность отклонения частоты выпадения «орла» от вероятности его появления меньше, чем на О. 1

Решение

В этом примере мы имеем дело с последовательностью испытаний Бернулли с параметрами р = 0.5 и п = 1200. Найдем искомую оценку по формуле (4):

                                                      05-05          025

                  —-05<Ol 21--                 — 0.979.

120012

ПРИМЕР 2

Пусть в результате 200 независимых опытов найдены значения случайной величины Х: д, Хь хм. Известно, что М(Х) 10 и D(X) = 2. Оценить снизу вероятность того, что абсолк:пная величина разности между средним арифметическим наблюдаемых значений случайной величины и математическим ожиданием будет меньше АП.

Решение

В лем примере для нахождения искомой оценки используем формулу (З):

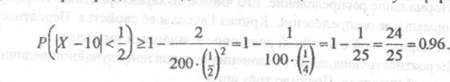
На угом мы завершаем наш краткий курс теории вероятностей. вы заинтересовались этой замечательной наукой, гораздо более полное и подроб- ное изложение её основ вы найдёте в учебниках, ссылки на которые содержатся в странице 50.

Авторы выражают надещду, что сведения и примеры, содержащиеся .в лом пособии, послужат вам в будущем (по крайней мере, на экзамене).

47