% ставка – это величина характеризующая интенсивность начисления % денег
Наращение – это увеличение суммы долга, за счет присвоения % денег
Коэффициент наращения – отношение наращенной первоначальной суммы (во сколько раз вырос первоначальный капитал)
Период времени – промежуток времени, в течении которого начисляется % денег
Интервал начисления – это минимальный период, за который начисляется % денег
2 способа начисления % денег:
1. Декурсивный метод (ссудный %). % начисляются в конце каждого интервала первоначального капитала. Интенсивность начислений определяет декурсивной % ставкой или ссудным %, который = отношению суммы % денег за год к первоначальному капиталу
В обоях способах начисляется %, может быть простым и сложным
В случаях простых % - % деньги не добавляются к первоначальной сумме и % деньги вычисляются в каждом интервале к первоначальной сумме
В случае сложных % - % деньги добавляются к первоначальному капиталу и исчисление % в следующем интервале осуществляется из наращенной суммы
Основные расчетные формулы при простых сложных ставках ссудного %
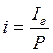 , где
, где
![]() - ставка ссудного %
- ставка ссудного %
![]() - годовая сумма % денег
- годовая сумма % денег
![]() - первоначальный капитал
- первоначальный капитал
![]() ;
; 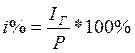
n- период начисления (в годах)
I – общая сумма % денег за весь период
I = P*i*n
S – наращенная сума
S = P+I=P*(1+i*n) = P (1+i*![]() /к)
/к)
1.
|
S = P*(1+i*n) |
Коэффициент наращения
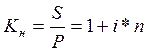
![]() – период начисления в днях к – количество дней в год
– период начисления в днях к – количество дней в год
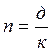
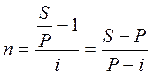
 - дисконтирование
- дисконтирование
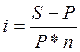 ;
; 
Нахождение наращенной суммы по известному первоначальному капиталу, называется операцией КОМПАУДИНГ S = P*(1+i*n)
Различные интервальные начисления
 , на каждом интервале свои %
, на каждом интервале свои %
Узнать Sn-?
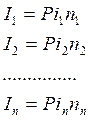
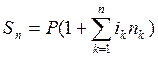
2.
|
|
Основные расчетные формулы при простых учетных ставках
d – учетная ставка
DГ – годовой % денег
S – наращенная сумма
D – за весь период начисления
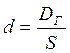 ;
; ![]()
![]()
![]()
![]()
3.
|
|
![]()

Задача:
S - 10
P - 5
n - 2
d - ?
![]() - дисконтирование
- дисконтирование
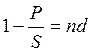
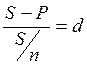
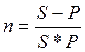
Основные расчетные формулы при сложных ссудных %
![]() - сложная ставка
ссудного %
- сложная ставка
ссудного %
![]() - сложный
коэффициент наращения
- сложный
коэффициент наращения
![]() - наращенная
сумма первого года
- наращенная
сумма первого года
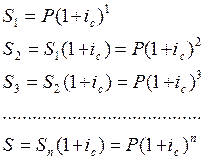
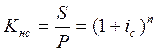
4.
|
|
Если интервалы разные
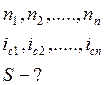
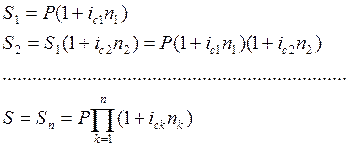
![]() - произведение
- произведение
Предположим, что интервалы одинаковы
 , тогда
, тогда ![]()
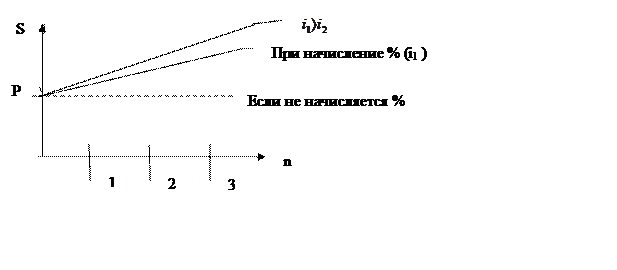
По формуле ![]() , при
, при ![]()
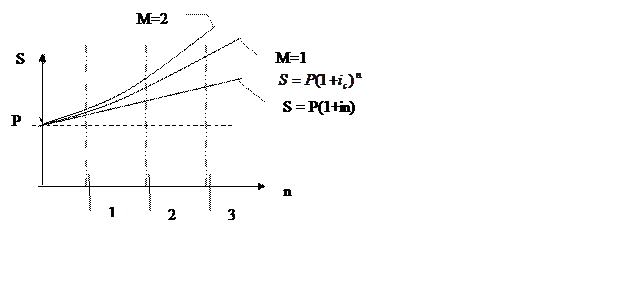
При увеличении начисленных чаще, чем годовые, тем выше уровень капитала
![]() - номинальная годовая ставка
ссудных %
- номинальная годовая ставка
ссудных %
![]() - количество интервалов
начисленных в году, тогда
- количество интервалов
начисленных в году, тогда
![]() - % ставка в каждом интервала
начисления
- % ставка в каждом интервала
начисления
4.
|
|
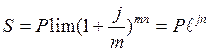
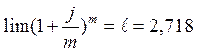
5.
|
|
Есть: S, P, i
Найти: n - ?
![]() , следует
, следует 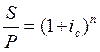

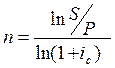
Есть: S, P, j, m
Найти: n - ?
 , следует
, следует

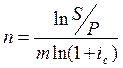
![]()
Из ![]()
![]()
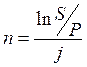
Есть: S, P, n
Найти: ![]() - ?
- ?
Из ![]() , следует
, следует
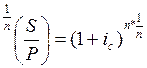
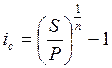
Есть: S, P, n, m
Найти: j - ?
Из  , следует
, следует
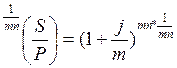
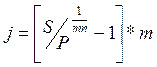
Из ![]() , следует
, следует

Через какой период времени удвоится первоначальное время?
![]() , найти – n - ?
, найти – n - ?
![]()

Существуют 2 правила:
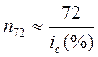
Если выдан кредит под 31 %
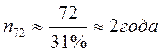
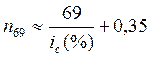
![]()
Основные расчетные формулы при сложных учетных ставках
![]() -
сложная учетная ставка
-
сложная учетная ставка
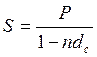

6.
|
|
![]() -
номинальная годовая учетная ставка
-
номинальная годовая учетная ставка
![]() - %
номинальная ставка на каждом интервале
- %
номинальная ставка на каждом интервале
7.
|
|
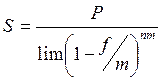
ПРЕДЕЛА НЕ СУЩЕСТВУЕТ
Задача:
![]() P= 5 000; m=4
P= 5 000; m=4
|
№ |
Формулы |
n=1 |
n=2 |
n=4 |
|
1 |
||||
|
2 |
||||
|
3 |
||||
|
4 |
||||
|
5 |
||||
|
6 |
||||
|
7 |
|
Есть: |
S, P, dc |
S, P, dc, m |
S, P, f, m |
S, P, n |
S, P, N, m |
|
Найти: |
n |
n |
n |
dc |
f |
29.04.04.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.