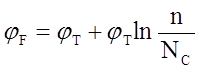Методические указания к практическим занятиям по дисциплине “Общая электротехника и электроника”, страница 3

Постоянство (“горизонтальность”) уровня Ферми в равновесной системе является одним из фундаментальных соотношений теории твердого тела. (Сами потоки  - дрейфовые и диффузионные могут быть, но они должны уравновешиваться). Потенциал Ферми для невырожденных полупроводников определяется выражениями:

(n – типа)

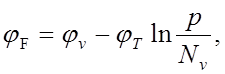                                                            ;          (8)

(p -типа)

(9)

т.е. у невырожденных полупроводников потенциал Ферми всегда лежит в запрещенной зоне; (логарифмы в обоих выражениях – отрицательны!).

С учётом того, что в диапазоне рабочих температур все донорные атомы ионизированы, можно считать, что

(полупроводник n-типа):   n = N_д , тогда концентрация свободных дырок (pn = n_i²)

p = n_i²/N_д .

С учётом приведённого выше

    

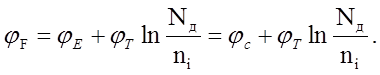
(10)

Отсюда следует, что уровень Ферми в электронном полупроводнике лежит тем выше, чем больше концентрация доноров и чем ниже температура.

Для дырочного п/п

P = N_a;

n = p_i²/N_a;

    

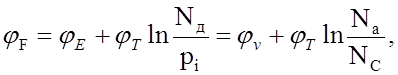
(11)

т. е. уровень Ферми лежит тем ниже, чем больше концентрация акцепторов и чем ниже температура.

р-слой                                           n-слой                                          

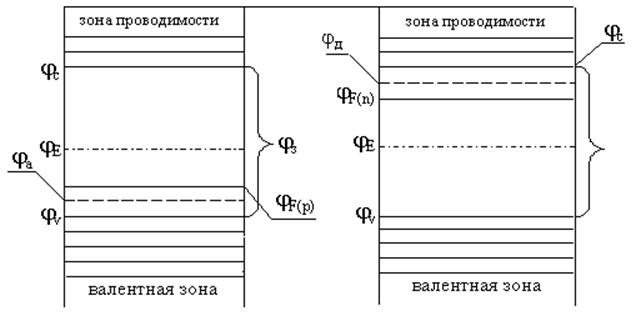
Тогда высота потенциального барьера при контакте p- и n- слоёв (контактная разность потенциалов):

                                                                                                                                                                                                                                                     

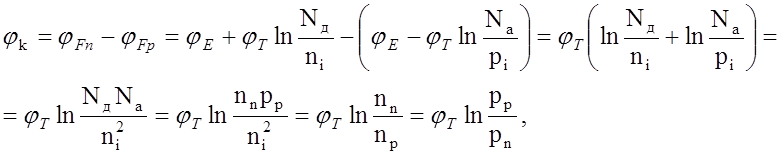
(12)

так как в равновесной системе уровень Ферми должен быть единым.

Из выражения 12 следует, что контактная разность потенциалов зависит от температуры и концентрации примесей в слоях p и n (от степени легирования слоёв).

          1. Определить положение уровня Ферми в Ge n – типа при Т = 300 К, если на 2*10⁶ атомов Ge приходится один атом примеси (донорная). Концентрация атомов в Ge равна 4,4*10²⁸ ат/м³ (N). Постоянная G в выражении, связывающем число электронов в единице объёма в зоне проводимости с температурой и энергетическими уровнями, равна 4,83*10²¹ м^-3*К^-3/2 (Ge). Ширина запрещённой зоны Е_з = 0,72 эВ, а расстояние между дном зоны проводимости и донорным уровнем 0,01 эВ.

Решение

Концентрация электронов в зоне проводимости определяется выражением

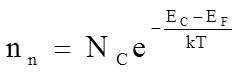, где                                                     (1)

Е_F – энергия уровня Ферми;

Е_С – энергия нижней границы зоны проводимости;

k – постоянная Больцмана;

Т – температура;

N_C – эффективная плотность состояний в зоне проводимости.

В свою очередь

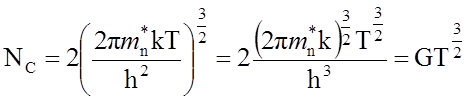, где               (2)

h – постоянная Планка;

 - эффективная масса электрона;

G -  коэффициент пропорциональности.

Перепишем выражение (1) в виде:

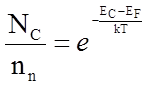 или 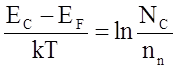, откуда

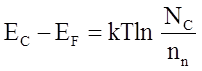,                                                                 (3)

что и будем анализировать.

Поскольку концентрация атомов в Ge N = 4,4*10²⁸ м^-3 и на 2*10⁶ атомов Ge приходится один атом примеси, а при температуре 300⁰ К разница между донорными   уровнями   и   дном   зоны   проводимости   равна   0,01   эВ   при  Е_д = 0,72 эВ; можно считать, что все атомы доноров будут ионизированы, тогда число свободных электронов в нём составит

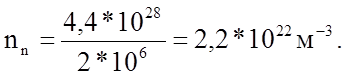
Эффективная плотность состояний в зоне проводимости при 300⁰ К из выражения (2)

.

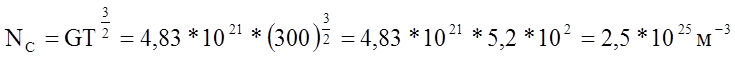Из выражения (3) окончательно имеем

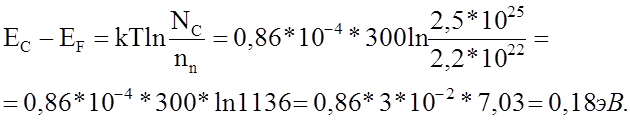
Таким образом, уровень Ферми находится ниже дна зоны проводимости на 0,18 эВ, что составляет 25 % от ширины запрещённой зоны.

2.       Вычислить положение уровня Ферми относительно дна зоны проводимости при температуре 400⁰ К для кристалла Ge, содержащего 5*10²² атомов сурьмы в м³.

Решение

Сурьма по отношению к германию является донором, германий будет n-типа, поэтому можно воспользоваться всеми рассуждениями и математическими выкладками  из предыдущей задачи.