Методические указания к практическим занятиям по дисциплине “Общая электротехника и электроника”, страница 2

                                                                   

                                                                    уровни валентная зона                    валентная зона       акцепторов             валентная зона

 

собственный п/п                п/п n-типа при 0 К                            п/п р-типа при 0 К

при Т > 0 К

Донорная примесь характерна тем, что её валентные уровни располагаются в верхней половине запрещенной зоны, все эти уровни заполнены при 0 К.

Акцепторная примесь характерна тем, что её валентные уровни располагаются в нижней половине запрещенной зоны, все они пусты при 0 К. Переходы электрона с донорного уровня в зону проводимости или из валентной зоны на акцепторный уровень требует сравнительно небольшой энергии. Поэтому примесная проводимость оказывается намного больше собственной (однако при достаточно высокой температуре проводимость всегда бывает почти собственной).

Уровень Ферми

Вероятность нахождения электрона на том или ином энергетическом уровне дается распределением Ферми-Дирака:

 

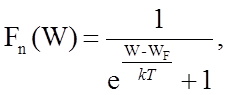
(1)

где k –  постоянная Больцмана;

T – абсолютная температура;

W_F – энергия, называемая уровнем Ферми.

Энергия уровня Ферми W_F соответствует такому энергетическому уровню, вероятность заполнения которого равна ½.

Удобнее выражать энергию не в джоулях, а в электрон-вольтах или просто в вольтах (т.к. численно они одинаковы).

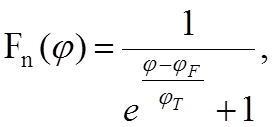Для этого поделим энергии на элементарный заряд, тогда

где j  -  потенциал, характеризующий энергиюW;

j_F – уровень Ферми;

j_т – температурный потенциал, равный

 

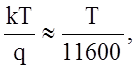q – заряд электрона.

Полезно запомнить, что при температуре 300 К (комнатная температура) j_т(300) » 0.025 В =  25 мВ.

В невырожденных полупроводниках уровень Ферми всегда лежит в запрещенной зоне. Глубину его залегания можно характеризовать “расстоянием” от одной из разрешенных зон, выраженных в единицах температурного потенциала j_т.

В большинстве случаев уровень Ферми залегает глубоко, т.е. выполняются неравенства:

j_с - j_F >> j_т ;                          (2)

j_F - j_v >> j_т,                       (3)

где j_с и j_v – потенциалы “дна” зоны проводимости (conduction) и “потолка” валентной зоны (valance).

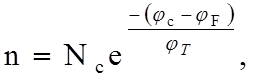Учитывая выражение (2) концентрация свободных электронов в зоне проводимости определяется как где              (4)

 

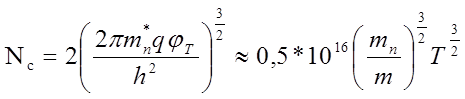- это эффективная плотность состояний (на см³) в зоне проводимости.

m^*_n - эффективная масса электрона.

Аналогично с учетом (3) концентрация свободных дырок в валентной зоне

 

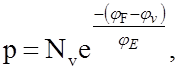
где     (5)

 

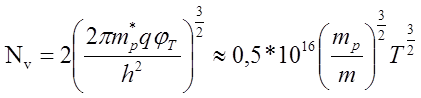- это эффективная плотность состояний в валентной зоне (на 1 см³);

m^*_p -    эффективная масса дырки.

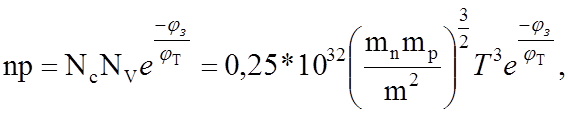Легко убедиться, что произведение концентраций np = n_i² = p_i² не зависит от положения уровня Ферми и определяется только температурой и шириной запрещенной зоны:

(6)

где j_з = j_c - j_v – ширина запрещенной  зоны,

n_i = p_i – концентрации собственных носителей.

Из соотношений (4) и (5) получим

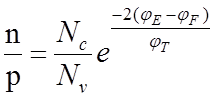                                                         (7)

 

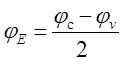где                - потенциал середины запрещенной зоны, который иногда называют электростатическим потенциалом п/п.

Потенциал Ферми имеет еще одно название – электрохимический потенциал. Градиент потенциала Ферми, будучи суммой градиентов электрического и химического потенциалов, позволяет одновременно характеризовать оба типа движения носителей – диффузию (химический) и дрейф (электрический). Следовательно, в условиях равновесия, когда направленного движения носителей нет, должно иметь место условие

 

 

то есть