2.6. Измерение меняющихся параметров во времени параметров
К параметрам, меняющимся во времени, относятся координаты цели. Варианты решения данной проблемы:
- Следящий измеритель
- Фильтрация параметров сигналов (оценивание меняющегося во времени параметров).
Реализация первого варианта:
Нам необходим :
![]()
В режиме слежения в следящем измерителе есть опорное значение, близкое к истинной величине a0. Разложим Y(t)в ряд Тейлора в окрестности a0 Возьмем три первых члена ряда:
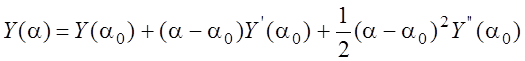
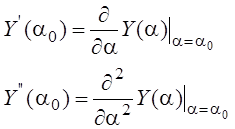
Уравнение правдоподобие:
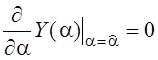
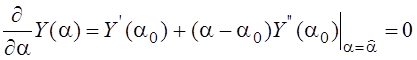
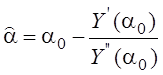
Нас интересуют ошибка рассогласования между оценкой и опорным значением:
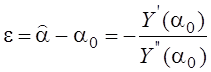
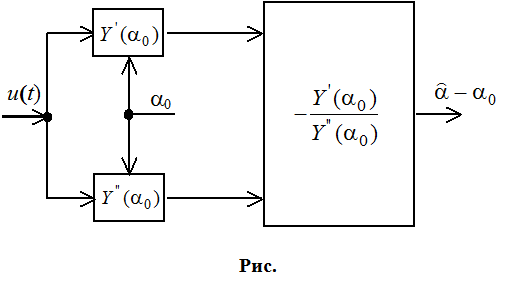
![]()
Cигнал ошибки:
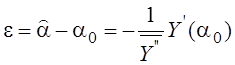
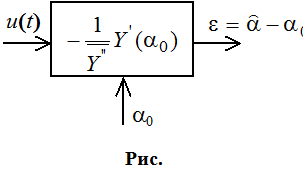
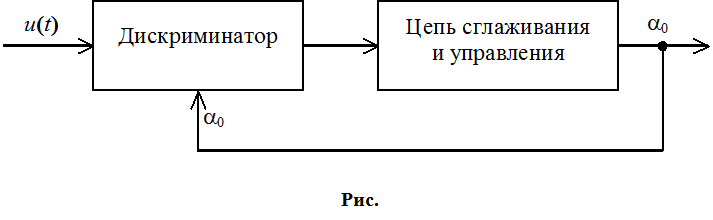
Подадим сигнал ошибки на цепь сглаживания и управления и запишем цепь обратной связи. Получим следующий измеритель:
Допустим
увеличился параметр a значит
увеличится сигнал ошибки (e)
через цепь обратной связи ![]() он
уменьшится таким образом происходит слежение, а в качестве измеренной величины
используют a0 (она
сглажена). На выход можно включить сумматор:
он
уменьшится таким образом происходит слежение, а в качестве измеренной величины
используют a0 (она
сглажена). На выход можно включить сумматор:
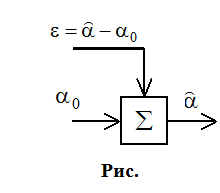
![]() - не содержит динамической
ошибки (то есть запаздывания за счет сглаживания), но она
содержит флуктуационную ошибку (шумовую). Сначала происходит
поиск потом захват затем слежение.
- не содержит динамической
ошибки (то есть запаздывания за счет сглаживания), но она
содержит флуктуационную ошибку (шумовую). Сначала происходит
поиск потом захват затем слежение.
Следующий измеритель запаздывания t:
![]()
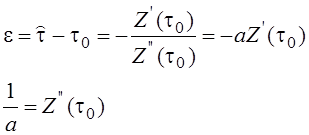
Возьмем
опорный сигнал: ![]() и
вычислим интеграл:
и
вычислим интеграл:
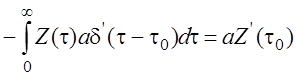
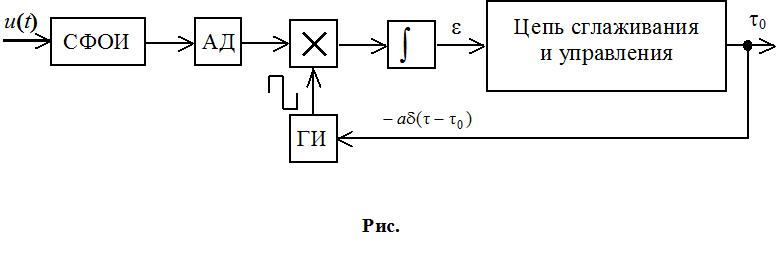
Реализация второго варианта:
u(t)=s[t,a(t)]+n(t) -
смесь помехи и сигнала. Нужно найти ![]()
Если ![]() , то фильтрация параметра
, то фильтрация параметра
Если ![]() , то сглаживание или
интерполяция
, то сглаживание или
интерполяция
Если ![]() , то экстраполяция (прогнозирование)
– фильтр Винера.
, то экстраполяция (прогнозирование)
– фильтр Винера.
Критерий предполагающий воспроизведение формы сигнала:
![]()
Если параметры связаны линейно (s=a), то фильтр линейный. Рассмотрим дискретный сигнал, когда сигнал сам является параметром (si=ai , ni=ai+ni); Отсчеты зависят от времени. Используется фильтр Кальмана:
Реализован
фильтр Кальмана для дискретных отсчетов. Данный фильтр является линейным, где
![]() - весовые
коэффициенты.
- весовые
коэффициенты.
Сигналы могут сливаться в один. Поэтому их необходимо различать. Введем понятие разрешающая способность. Разрешающая способность для времени запаздывания – это минимальное расстояние на котором два сигнала можно увидеть раздельно. Это необходимо когда мы сопровождаем множество целей. Задача разрешения – многоальтернативное обнаружение. Пусть n=2 , тогда нужно проверить четыре гипотезы:
1. Наблюдается две цели.
2. Наблюдается первая цель.
3. Наблюдается вторая цель.
4. Целей нет.
Если мы обнаружили и знаем количество целей, то можно заняться задачей определение координат целей.
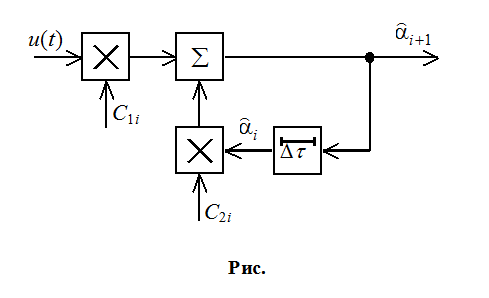
Зондирующий согнал:
s0(t)-
огибающая, ![]() - угловая
модуляция (частотная или фазовая).
- угловая
модуляция (частотная или фазовая).
Гильбертова огибающая:
![]()
![]()
![]()
Гильбертова комплексная огибающая:
![]()
Отраженный сигнал (без шумов и учета ослаблении в атмосфере).
![]()
![]() - частота Доплера
- частота Доплера
t- время задержки
Нормированная двумерная АКФ нашего сигнала.
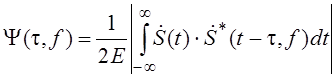
Частотно – временная функция неопределенности:
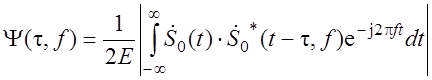
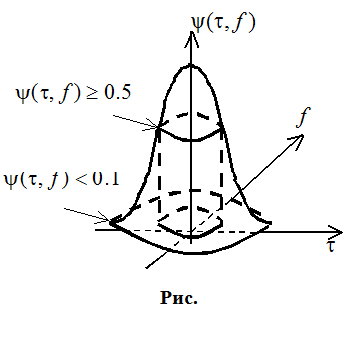 Фаза не нужна так как
стоит модуль. Функция неопределенности имеет пространственный характер – это
поверхность. Причем ее максимум находится в точке
Фаза не нужна так как
стоит модуль. Функция неопределенности имеет пространственный характер – это
поверхность. Причем ее максимум находится в точке ![]() и равен
и равен ![]() .
.
Чем быстрее
спадает тем разрешение лучше. Возьмем сечение f=0
![]() , для импульса:
, для импульса:
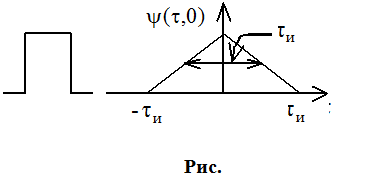
Возьмем
сечение t=0 ![]() - определяет разрешение по
частоте. Это будет спектор нашего импульса.
- определяет разрешение по
частоте. Это будет спектор нашего импульса.
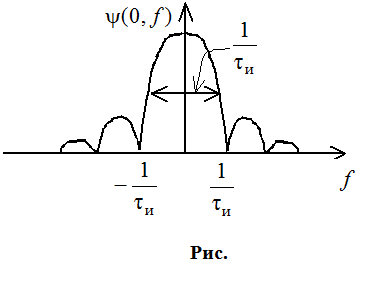
Объем под функцией неопределенности называется телом неопределенности (V). Его можно рассчитать по формуле:
V=const – всегда и не зависит от параметра сигнала – сущность
принципа неопределенности. То есть если мы сожмем его по одной координате,
то он расширяется по другой координате. С уменьшением t мы улучшим разрешение по дальности, но
одновременно увеличится ![]() и
ухудшится разрешение по скорости. Справедливо и обратное высказывание. Обычно
используют проекции сечений функции неопределенности на плоскость. Берется
область высокой корреляции:
и
ухудшится разрешение по скорости. Справедливо и обратное высказывание. Обычно
используют проекции сечений функции неопределенности на плоскость. Берется
область высокой корреляции:
![]()
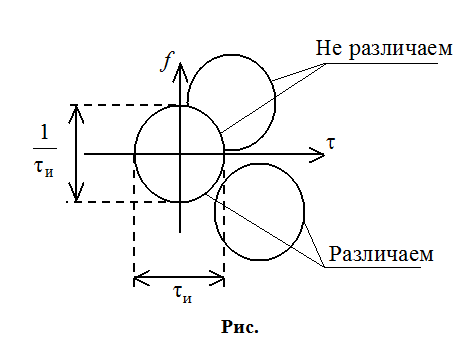
Если сигналы
перемешаются в области высокой корреляции, то их не различить. ![]() - принцип неопределенности
для простых сигналов, то есть происходит улучшение одного параметра за счет
другого.
- принцип неопределенности
для простых сигналов, то есть происходит улучшение одного параметра за счет
другого.
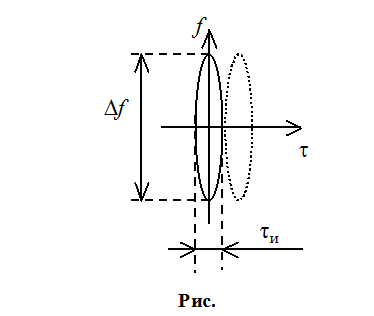
По длительности разрешение
улучшаем за счет ![]() :
:
По частоте разрешение улучшено за счет времени.
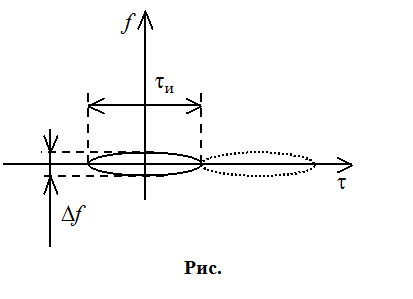
Для когерентной пачки, диаграмма неопределенности имеет периодический характер. Однозначность определяется по Tп (по дальности).
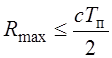
Двойка в знаменателе говорит о то, что сигнал проходит два расстояния: от антенны до цели и обратно.
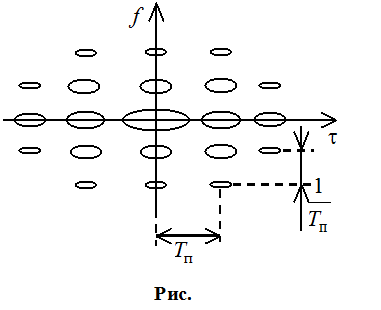
Однозначность
по частоте определяется 1/Тп . Из-за того что цель может
лететь как на нас, так и от нас, то 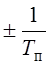
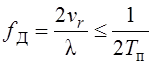 ;
; 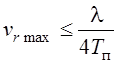 ;
; 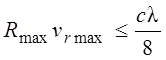
То есть можно измерить одну координату за счет другой. Чтобы увеличит однозначность нужно увеличить длину волны, то тогда увеличатся геометрические размеры антенны. Можно нарушить интервал неопределенности Тп1Тп2то есть интервал неопределенности будет равен:
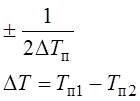
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.