3.2. Сложные сигналы
Для повышения
разрешающей способности по дальности нужно уменьшить ![]() . Но тогда уменьшается энергия
. Но тогда уменьшается энергия
![]() и как следствие
уменьшиться отношение сигнал/шум:
и как следствие
уменьшиться отношение сигнал/шум:
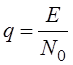
Скомпенсировать
уменьшение энергии путём повышения ![]() нельзя
так как она ограничена мощностью пробоя фидера. Выходом из сложившейся ситуации
является использование сложных сигналов:
нельзя
так как она ограничена мощностью пробоя фидера. Выходом из сложившейся ситуации
является использование сложных сигналов:
![]()
1. Сложные сигналы с линейно-частотной модуляцией (ЛЧМ).
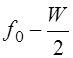 ;
; 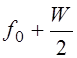 , где W
– дивиация частоты
, где W
– дивиация частоты
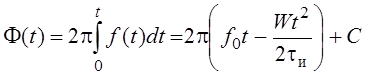 ; С=0 так как Ф(0)=0
; С=0 так как Ф(0)=0
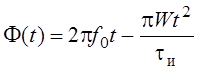

![]()
![]()
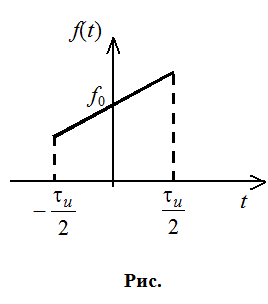
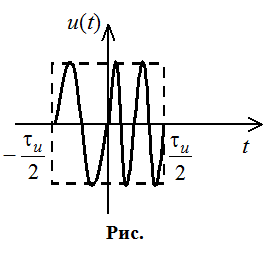
АКФ ЛЧМ – сигналов:
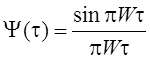
Ширина
спектра модулирующего сигнала: ![]() .
Если
.
Если 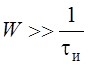 ,то
,то ![]()
Пусть мы имеем сложный сигнал:
![]()
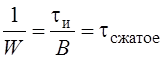
Таким образом
ЛЧМ – сигнал может сжиматься в СФ. Тогда разрешающая способность будет
определятся ![]()
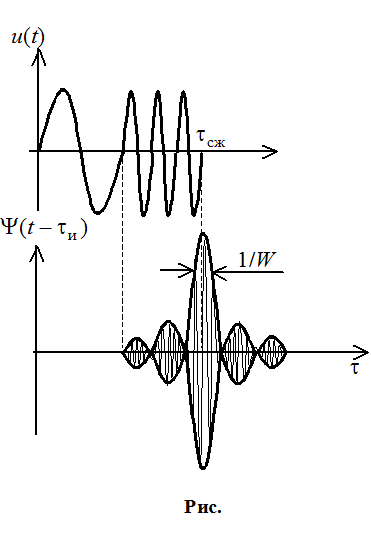
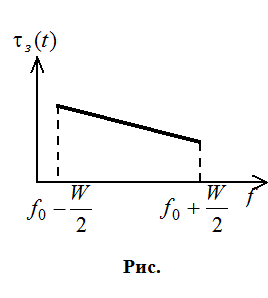
Недостаток
боковые лепистки. Энергия опредешяется исходной длительностью импульса - ![]() , а разрешение -
, а разрешение - ![]() .
.
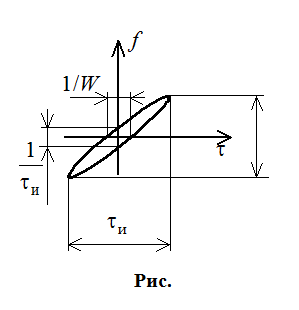
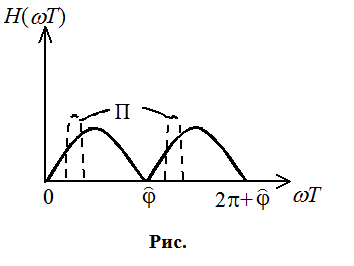
Расширить различение по t и по f одновременно. Наилучшая ситуация – рис. . Наихудшая ситуация – рис. .
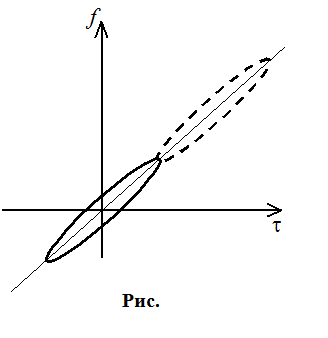
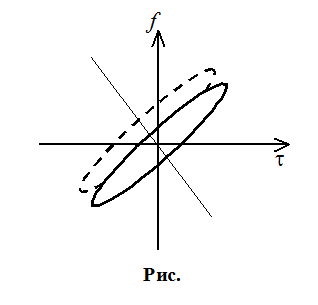
Недостатки:
1.
2. Смещение импульса на fД
Второй недостаток исправляют путём введения второго сигнала.
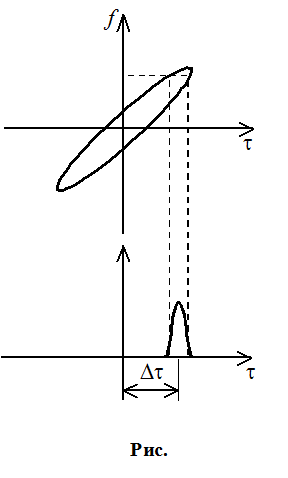
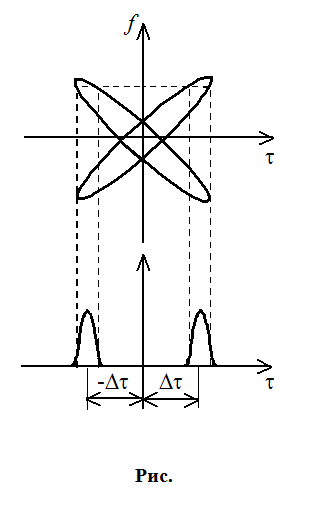
За счет двух сигналов можно скомпенсировать добавку и узнать истинное положение сигнала.
2. Лучший сигнал должен иметь «кнопочную» форму функции неопределенности. Такие сигналы фазоманипулированные (ФМ).
![]()
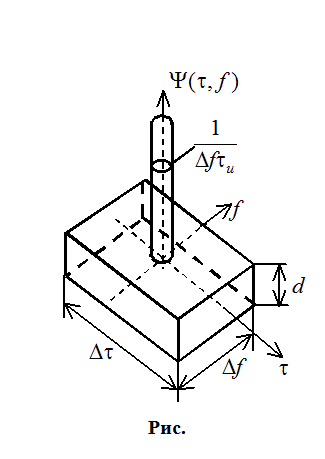
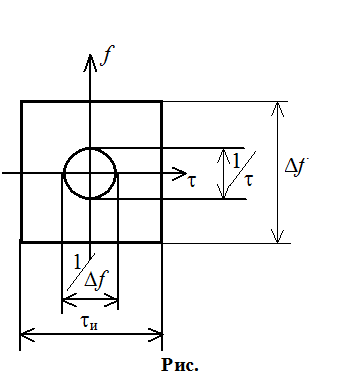
Разрешение определяется не длительностью сигнала, а шириной его спектра:
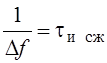
Найдем объем
пика тела неопределенности. Его высота равна единице, а основание - 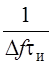 , следовательно:
, следовательно:
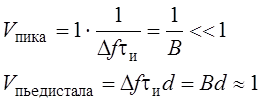
Высота боковых лепестков:
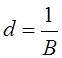
d – высота боковых лепестков (максимальная), которая получается при сжатии.
ФМ – импульсный сигнал, длительностью tи , состоит из n элементарных сигналов длительностью t1:
![]()
Все сигналы отличаются комплексными амплитудами:
![]() , где i=1,2,…, n
, где i=1,2,…, n
Эти комплексные амплитуды образуют кодовые комбинации. Простейший сигнал – двоичный однофазный сигнал:
![]() , когда
, когда ![]()
![]() , когда
, когда ![]()
Если начальная фаза (j) принимает и другие значения, то это будет многофазный сигнал. Для кодирования используется код Баркера:
![]()
Пусть n=7 :
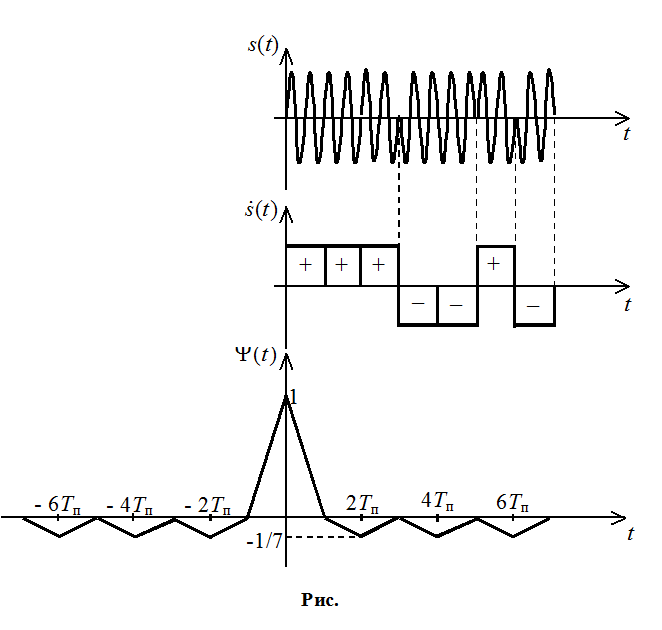
Сожмем сигнал
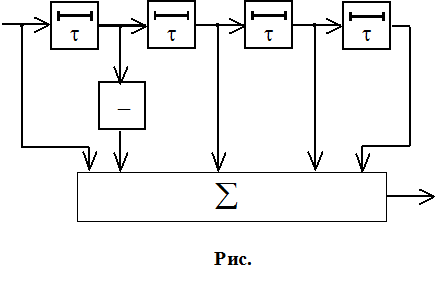
при n=5 (используется ЛЗ с отводами –
практически не реально, так как очень широкая полоса). Весовые коэффициенты в
отводах ЛЗ: 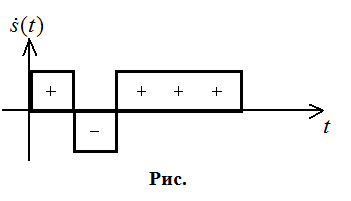
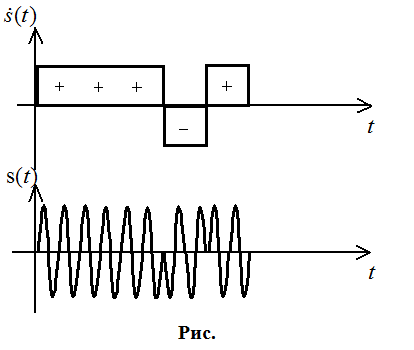
Весовые коэффициенты на СФ – зеркально отображенные.
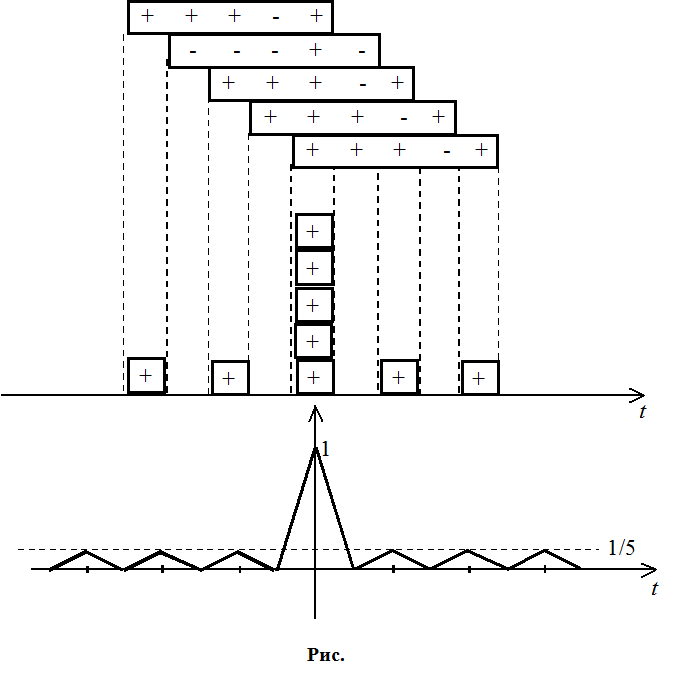
Обычно коды
Баркера ![]() , если
, если ![]() ,то используется M последовательности, в
них боковые импульсы могут быть больше отношения 1/n.
Реально можно сжимать с помощью корреляционного фильтра, многоканального по
дальности, то есть в каждом канале используется опорный сигнал. Существуют
также многофазные сигналы, где фаза принимает свои значения дисперсно на
интервале
,то используется M последовательности, в
них боковые импульсы могут быть больше отношения 1/n.
Реально можно сжимать с помощью корреляционного фильтра, многоканального по
дальности, то есть в каждом канале используется опорный сигнал. Существуют
также многофазные сигналы, где фаза принимает свои значения дисперсно на
интервале ![]() и
частотно-модулированные – дисперсном изменением частоты. Была рассмотрена
внутренняя модуляция, возможна и межимпульсная модуляция.
и
частотно-модулированные – дисперсном изменением частоты. Была рассмотрена
внутренняя модуляция, возможна и межимпульсная модуляция.
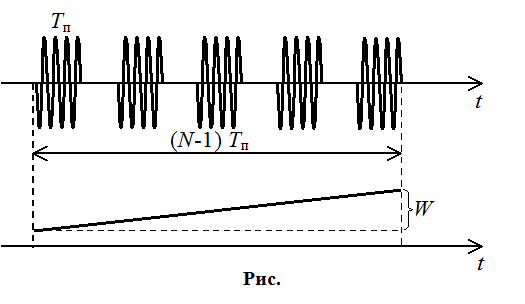
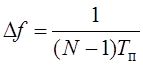
1/W – различение по дальности. ![]() разрешение
можно получить десятки сантиметров.
разрешение
можно получить десятки сантиметров.
3.3. Априорная неопределённость и методы её определения
В реальных условиях априорное полное статистическое описание сигнала отсутствует. Для белого шума неизвестна дисперсия, для пассивной помехи неизвестна спектрально-корреляционная характеристика, для активной помехи неизвестна спектрально-корреляционная характеристика, а также закон распределения, для сигнала неизвестны начальная фаза, амплитуда, энергетический спектр. Отсутствие априорных сведений о сигнале называют априорной неопределенностью.
Неопределенности делятся:
- Параметрическая
- Непараметрическая
Если известны
закон распределения ![]() , а
неизвестны параметры помехи и сигнала, то это параметрическая неопределенность.
Если неизвестен хотя бы один закон распределения, то данная неопределенности –
непараметрическая.
, а
неизвестны параметры помехи и сигнала, то это параметрическая неопределенность.
Если неизвестен хотя бы один закон распределения, то данная неопределенности –
непараметрическая.
Методы преодоления априорной неопределенности:
1. Методы адаптации (при параметрической и непараметрической неопределенности)
2. Непараметрический метод (при непараметрической неопределенности)
3. Робастный метод (при параметрической и непараметрической неопределенности)
1. Метод адаптации :
В основе адаптации лежит процесс обучения, при котором определяются оценки неизвестных характеристик (закон распределения) и параметров. Использование оценок при обработке к адаптивному алгоритму. При параметрической неопределенности, в алгоритм обработки неизвестные параметры заменяются состоятельными оценками (оценками максимального правдоподобия).
Пусть
неизвестный параметр для белого шума – дисперсия (![]() ):
):
![]()
![]()
Таким образом можно поступать практически с любым параметром. Схема адаптивного устройства (схема с прямыми связями):
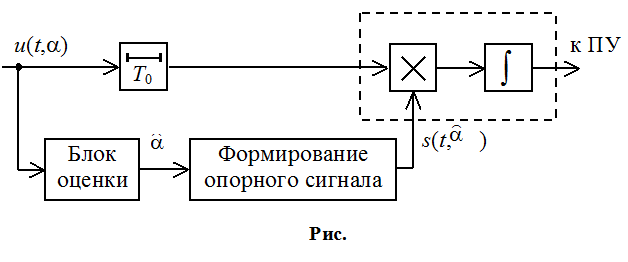
T0 - компенсирует задержку в блоке оценки и в блоке формирования опорного сигнала.
ЧПК-1
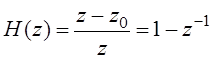
![]()
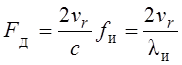 , где vr-
радиальная скорость
, где vr-
радиальная скорость
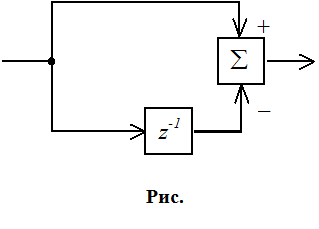
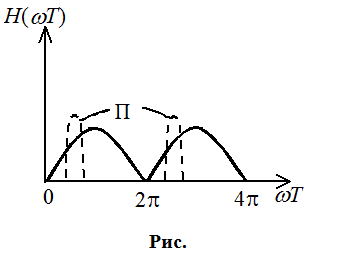
Нужно найти ![]() и повернуть ноль АЧХ на этот
угол, для этого нужно z0 умножить на exp(jj).
и повернуть ноль АЧХ на этот
угол, для этого нужно z0 умножить на exp(jj).
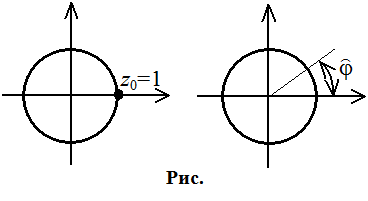
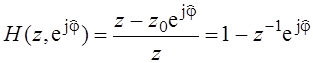
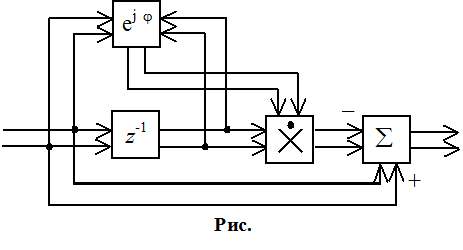
Адаптивный режекторный фильтр:
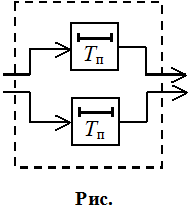
![]()
![]()
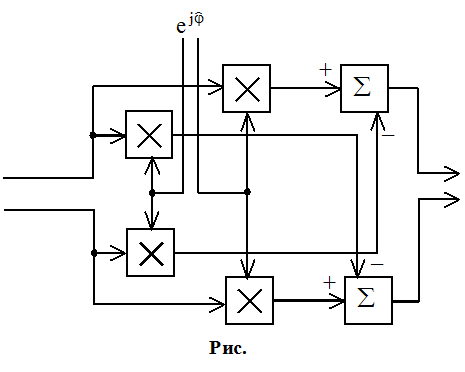
![]() -
определяется непосредственно по помехе.
-
определяется непосредственно по помехе.
2. Непараметрический метод:
Применяется при непараметрической априорной неопределенности. Используются знаковые, порядковые, ранговые методы. Дискретные отсчеты входных данных: u(ti)=ui. Вычисляются sing(ui):
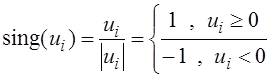
sing(ui) – знаковая функция (определяет только знак), тогда после преобразования останется только знак.
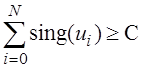
Пусть помеха имеет неизвестный симметричный закон:
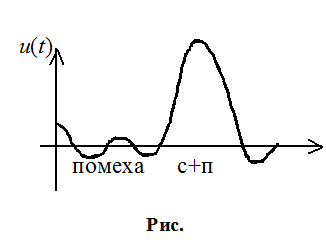
Такой закон инвариантен к закону распределения помехи.
3.Робастные методы:
Используются алгоритмы устойчивые к изменению характеристик, то есть параметры, например, помехи меняются, а характеристики сохраняются.
Сначала строится алгоритм на наихудшую помеху, например, на наименьшую вероятность правильного обнаружения. Для других вероятностей он будет давать результаты не хуже. Делают усечение выборки:
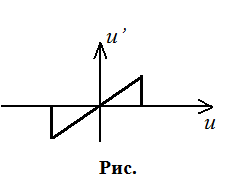
Винзарирование выборки (ограничение выборки):
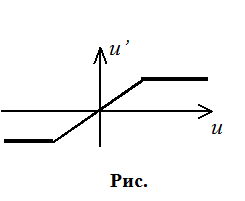
Цензурирование – все выборки располагают в порядке возрастания , а первую и последую отбрасывают.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.