Содержание.
1. Различение сигналов
1.1 Статистические критерии различения сигналов
1.2 Правило оптимального различения
1.3 Функция правдоподобия при различении сигналов на фоне нормального
шума
1.4 Различение двух сигналов
1.5 Полная вероятность ошибки при различении двух сигналов
1.6 Различение М сигналов
1.7 Обнаружение М сигналов с неизвестной начальной фазой
2. Оценивание параметров сигнала
2.1 Критерии оценки параметров сигнала
2.2 Функционал правдоподобия при оценки параметров сигнала.
2.3 Оценка энергетических параметров. Оценка амплитуды сигнала
2.4 Оценка неэнергетических параметров. Оценка времени запаздывания
2.5 Оценка частоты и совместная оценка времени запаздывания частоты
2.6 Измерение меняющихся параметров во времени параметров
3. Разрешение сигналов
3.1 Функция неопределённости
3.2 Сложные сигналы
3.3 Априорная неопределённость и методы её определения
1.1. Статистические критерии различения сигналов
Пусть есть множество из М сигналов: s={s1(t), s2(t),…, sM(t),} Пусть по каналу передаётся только один сигнал: si(t), i=1,2,..,M. u(t)= si(t)+n(t) , где n(t)-шум. Различение состоит в операции (обработке) над принятым колебанием u(t) с целью вынесения решения – какой сигнал сигнал был принят.
Обнаружение – частный случай различения двух сигналов, когда один сигнал нулевой. Каждому сигналу соответствует гипотеза Hi (i=1,2,…,M). После различения принимается решение Ak (k=1,2,…,M).
Различение - многоальтернативная проверка гипотез, а обнаружение – двухальтернативная проверка гипотез. Универсальным критерием является критерий минимума среднего риска – критерий Байеса. Предполагается наличае c вероятностью pi сигнала si(t) в выходном колебании u(t). pi– априорная вероятность (определяется средней частотой посылки сигнала) pi– априорная вероятность гипотезы Hi
pi=P(Hi) 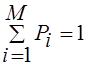 H1, H2,
H3,…, HM
- полная группа событий
H1, H2,
H3,…, HM
- полная группа событий
Условная вероятность перепутывания i-ого и k-ого сигналов : pik=P(Ak/Hi) – вероятность того что принимается решение Ak о передаче сигнала sk(t), при условии, что на самом деле истинная гипотеза Hi , то есть передан сигнал si(t). pik – характеризует вероятность всех ошибочных решений. Ошибочному решению соответствует совмещенное событие AkHi , вероятность которой:
P(AkHi) = P(Hi) P(Ak/Hi) = pi pik
P(Hi) - априорная вероятность, P(Ak/Hi) - условная вероятность. Каждому совмещённому событию и его вероятности соответствуют риски (потери) – rik . Всего таких рисков – M2. Но rii=0 то есть при правильном различении риски отсутствуют. Средний риск:
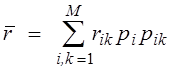
Критерий
Байеса: ![]() Пусть rik = r (для простоты
), тогда
Пусть rik = r (для простоты
), тогда
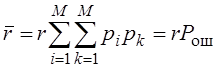
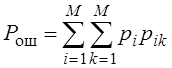
Полная вероятность ошибки при различении сигналов.
![]()
Критерий идеального наблюдателя критерий Котельникова – частный случай критерия Байеса. Будем считать, что все сигналы равновероятны, тогда
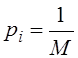
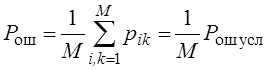
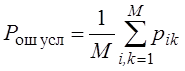
Условная полная вероятность ошибки
![]()
вариант критерия идеального наблюдателя
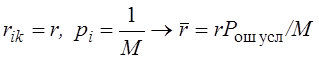
Рассмотрим М детерминированных сигналов, при наличие помех, статистические свойства которых нам известны. Hi – гипотеза, при условии что был передан сигнал si(t). Выходное колебание: u(t)= si(t)+x(t) , где x(t)-помеха. Условная плотность вероятности: W[u(t)/Hi] – известна. Пусть пространство в котором наблюдается сигнал u(t), будет разбито на М областей: V1, V2,…, VM им соответствуют решения А1, А2,…, АM . Различение сводится к определению области в которую попало наше колебание.
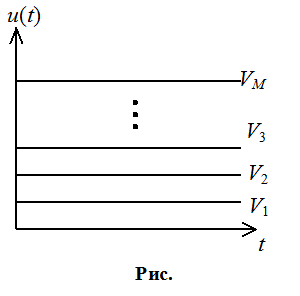
Если попало колебание в область Vk , то принимается решение Ak , о том что передан сигнал sk(t). Оптимальность различения заключается – в оптимальном различении этих областей. Будем искать оптимальность по критерий Котельникова (по Рош или Pош усл). Нам нужны условные вероятности перепутывания сигналов:
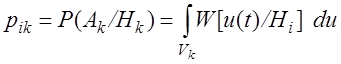
Это вероятность того, что наш сигнал si(t) находится в области Vk
. Чтобы ![]() необходимо
чтобы
необходимо
чтобы ![]() . Для
этого должны быть максимальны вероятности правильного различения , что
достигается в случае наиболее правдоподобных решений Ак по
правилу:
. Для
этого должны быть максимальны вероятности правильного различения , что
достигается в случае наиболее правдоподобных решений Ак по
правилу:
![]() i = 1,2,…,M
i = 1,2,…,M
Ак
Данная
формула – правило оптимального различения. Для принятой реализации u(t) нужно выбрать только
решение Ак при котором данная вероятность будет максимальна.
Это и будет оптимальным правилом. При pi=1/М
мы приходим к такому критерию ![]() .
Тогда правило оптимального различения:
.
Тогда правило оптимального различения:
![]() , i =
1,2,…,M
, i =
1,2,…,M
Ак
W[u(t)/Hi] - Условная плотность вероятности . Определяется как при условии истинности гипотезы Нi для принятой реализации u(t) , является функцией номера i и называется функцией (функционалом) правдоподобия. В случае оптимального различения осуществляется по максимальному правдоподобию, при котором для принятой реализации u(t) принимается решение Ак об истинности гипотезы Нк при котором функционал правдоподобия будет максимальным. У сигналов может быть неизвестным параметр ai тогда:
W[u(t)/Hi , ai] - неизвестным параметр исключают усреднением:
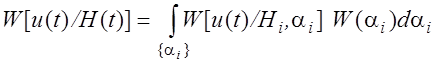
1.3. Функции правдоподобия при различении сигналов на фоне нормального шума
Пусть нужно различить сигнал на фоне нормального (гауссовского) шума. Гипотезе Нi соответствует u(t)= si(t)+n(t), где i = 1,2,…,M , тогда n(t)= u(t)-si(t)
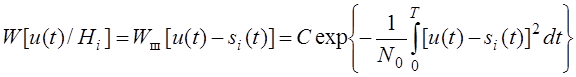
По правилу максимального правдоподобия мы должны принять решения о таком si(t) , для которого функционал правдоподобия будет максимальным. Нужно принять решение о наличие сигнала si(t) , который наименее уклоняется от u(t), а мерой уклонения является энергия разности u(t)-si(t). Раскроем скобки в функционале:
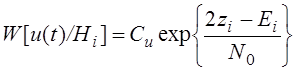
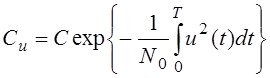
От i не зависит(в различении не участвует).
Корреляционный интеграл:
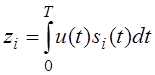
Корреляционный интеграл определяет сходство u(t) с si(t). Энергию i-ого сигнала можно вычислит по формуле:
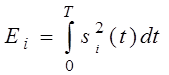
Функционал правдоподобия будет максимальным, при максимальном показатели экспоненты и минимальном корреляционном интеграле. Физическая сущность правила максимального правдоподобия: решение о наличие u(t) принимается для такого сигнала si(t) с которым u(t) имеет наибольшее сходство (корреляцию). У сигналов может быть неизвестным случайный параметр ai ,то есть сигнал квазидетерминированный. Но если использовать некоторое фиксированное значение, то получим детерминированный сигнал для этих значений.
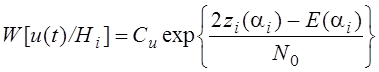
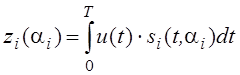
Корреляционный интеграл для конкретного значения ai :
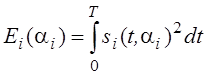
Энергия сигнала для конкретного значения ai (ai – величина неизвестная так как является случайной величиной). Усредним функционал правдоподобия по неизвестным величинам:
![]()
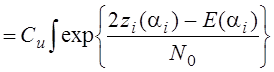
Обычно ai
– начальная фаза ![]() :
:
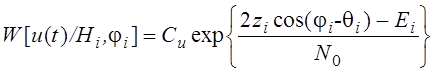
![]() , где
, где
![]() квадратурные составляющиекорреляционного интеграла
квадратурные составляющиекорреляционного интеграла
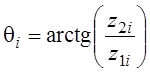
![]()
![]() то есть энергия одинаковая
то есть энергия одинаковая
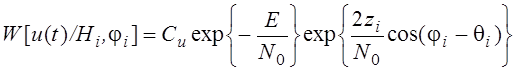
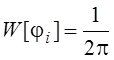 ;
; ![]()
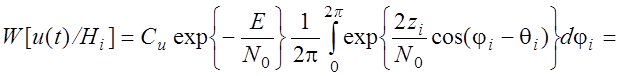
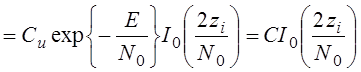 ,где
,где
I0 - Функция Бесселя.
На вход поступает колебание:u(t)= si(t)+n(t). По критерию ![]() нужно использовать правило
максимального правдоподобия.
нужно использовать правило
максимального правдоподобия.
![]()
А1
![]()
А2
p1=p2=1/М=1/2 Е1=Е2=Е
![]()
А1
![]()
А2
Пусть сигналы детерминированные, а шум нормальный белый. Тогда можно использовать корреляционный интеграл:
z1>z2 при решении А1 ; z1<z2 при решении А2
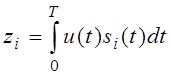
z = z1-z2>0 при решении А1 то есть принят сигнал s1(t)
z = z1-z2<0 при решении А2 то есть принят сигнал s2(t)
Два канала, каждый из которых настроен на ожидаемый сигнал:
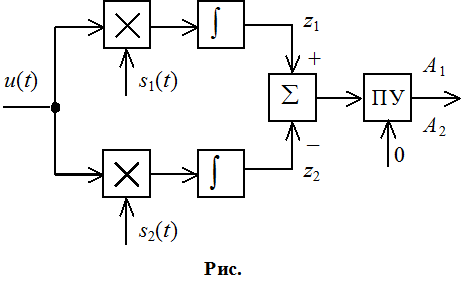
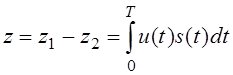
s(t) = s1(t)-s2(t)
Особенность различения коррелятора: необходимо знать время прихода сигнала.
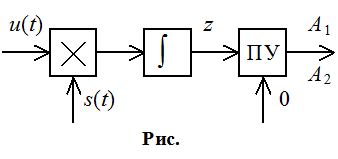
Коррелятор можно заменить СФ (импульсные характеристики согласованные с формой сигнала).
s1(t) импульсная характеристика s1( T-t )
s2(t) импульсная характеристика s2( T-t )
Тогда время прихода сигнала безразлично.
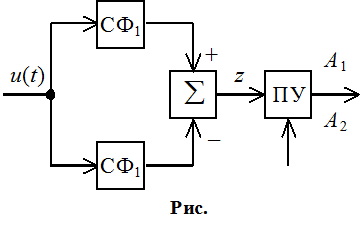
Можно построить фильтр с разностным сигналом s( T-t )
![]()
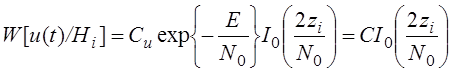
![]()
![]() , где
, где
![]() -
квадратурные составляющие корреляционного интеграла вычисляются на выходе СФ.
-
квадратурные составляющие корреляционного интеграла вычисляются на выходе СФ. ![]() - огибающая выходной величины
СФ (вычисляется с помощью амплитудного детектора).
- огибающая выходной величины
СФ (вычисляется с помощью амплитудного детектора).
p1=p2=1/2
![]()
А1
![]()
А2
Стоит отметить, что Zi>0 всегда.Функция Бесселя является монотонной функцией своего аргумента. Значит для различения можно использовать величины Z1 и Z2.
Z = Z1-Z2>0 при решении А1 то есть принят сигнал s1(t)
Z = Z1-Z2<0 при решении А2то есть принят сигнал s2(t)
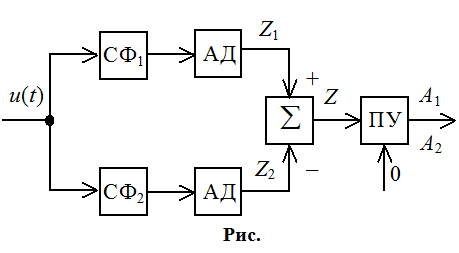
СФ позволяют различить сигналы с неизвестным временем прихода. Из-за шумов всё-таки происходят ошибки (перепутывания).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.