Критерии оценивания параметров сигнала. Функционал правдоподобия при оценки параметров сигнала

2. ОЦЕНИВАНИЕ ПАРАМЕТРОВ СИГНАЛА

2.1. Критерии оценивания  параметров сигнала

Оценивание – для алгоритмов обработки.

Измерение – более технический термин (применяется к структурным схемам).

Оценка – процедура, измеренная величина.

Пусть на интервале 0<t<T передаётся аддитивная смесь сигнала и помехи (шума): u(t) = s(t,{a_i}) + n(t),где {a_i} = {a₁,a₂,…,a_m} – вектор параметров сигнала. Пусть параметры a₁,a₂,…,a_m на отрезке t – не изменяются.

            Параметры сигнала могут быть:

               - Информационные (несёт ли сигнал полезную информацию: амплитуда,  частота, фаза, время запаздывания, угол прихода)

             -    Неинформационные (не несёт полезную информацию)

Оценивание – процедура или алгоритм при обработке принятого сигнала u(t) с целью вынесения решения о значениях параметра сигнала.

Измеренная величина -  - оценка параметра. Если у нас a(t), то процедура (оценивание) – фильтрация параметров сигнала. Если a- случайная величина с известным законом распределения, то можно использовать байесовский критерий: минимум среднего риска, то получим байесовские оценки. Вводятся стоимости ошибок или риски: при оценки – это непрерывные риски (функции). Которых существует большое разнообразие. Одна из самых распространённых:  . При такой функции критерий минимума среднего риска эквивалентен критерию минимума среднеквадратической ошибки: . Обычно распределение ошибки неизвестно, да и параметр не всегда случайная величина. Если оценки – действительная случайная величина, то используется не байесовские методы, наиболее известным из которых является метод максимального правдоподобия. Данный метод оперирует с функцией правдоподобия. Функция правдоподобия – W[u(t),a], которая для различения сигнала u(t), рассматривается как функция параметра a. Из этого метода получаются оценки максимального правдоподобия. Оценка максимального правдоподобия - такая величина , при которой функция правдоподобия максимальна.

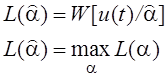
Удобно использовать натуральный логарифм так как в дальнейших преобразованиях будет экспонента. Уравнение правдоподобия запишется так:

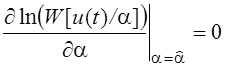
Проблема неинформационных параметров. Два пути решения:

              - Оценивать все параметры, а  оценки неинформационных параметров   отбрасывать.

             - Усреднять функцию правдоподобия по неинформационным параметрам.

Оценка  из-за погрешности измерения – случайная величина.  -смещение оценки. -(среднее смещение) характеризует систематическую ошибку. Если =0 то оценка называется несмещенной, иначе оценка называется смещенной. Для  называется несмещенной оценки матожидание оценки равно исходному параметру: . Оценка обычно зависит от количества отсчётов m по которым она определяется  (). Оценка  называется ассимптотически несмещенная если . Случайная погрешность характеризуется дисперсией оценки . Оценка эффективна, если её дисперсия меньше дисперсии любой другой оценки. Оценка ассимптотически эффективна, если её дисперсия минимальна при . Оценка состоятельна, если она сходится по вероятности к исходному значению параметра:

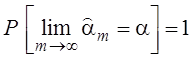
Если оценка – состоятельна, несмещенная и эффективная, то она оптимальна. Неравенство Рао-Крамера определяет нижнюю границу дисперсии несмещенной оценки (граница Рао-Крамера):

                                                                            

Вычислим с помощью функции правдоподобия. Меньше  - ошибка быть не может. Если для несмещенной оценки , то оценка эффективна. Оценки максимального правдоподобия для большинства случаев ассимптотически оптимальны они состоятельные несмещенные или  ассимптотически несмещенные и ассимптотически эффективны.

2.2. Функционал правдоподобия при оценки параметров сигнала.

На фоне аддитивного нормального белого шума функция правдоподобия имеет вид:

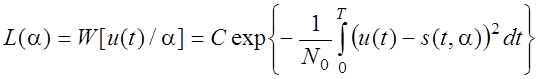
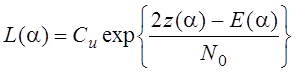   (1)

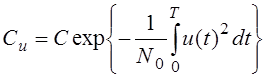- зависит только от u(t)

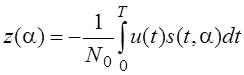    - корреляционный интеграл определяет

                   сходство u(t) и s(t,a)

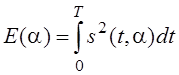   - энергия сигнала

«Правдоподобия» для принятой реализации u(t) зависит от сходства этой реализации с сигналом s(t,a) и энергией сигнала для данного значения  a.

Параметры бывают:

               -  Энергетические

               -  Неэнергетические

У вторых энергия сигнала от параметра не зависит E(a)=E, у первых такая зависимость есть. Если энергетический параметр сигнала равен нулю, то и сигнал равен нулю: a=0, то s(t,a)=0. пусть известен неэнергетический параметр - начальная фаза:

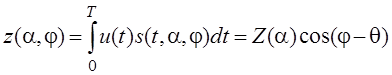
    , где   квадратурные составляющие

         корреляционного интеграла

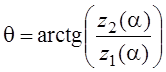
Энергия от начальной фазы не зависит , тогда функция правдоподобия будет иметь вид:

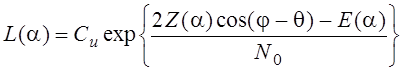
Если  - параметр меняющийся, то нужно найти усреднение:

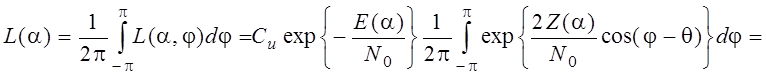
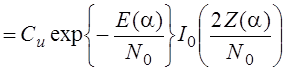
Правило максимального правдоподобия:

Если использовать формулу (1) достаточно взять показатель экспоненты, так как функция является монотонной от этого показателя. Тогда:

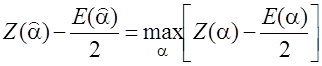                                 -  правило справедливо для           энергетических параметров. А для неэнергетических:

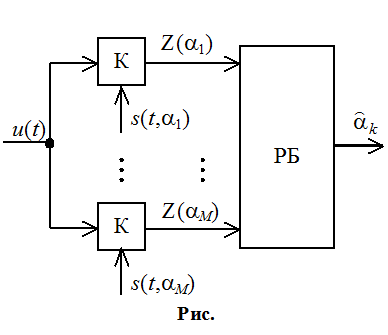
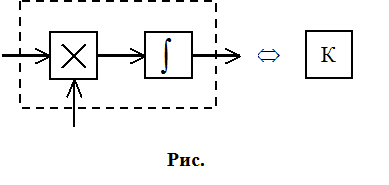
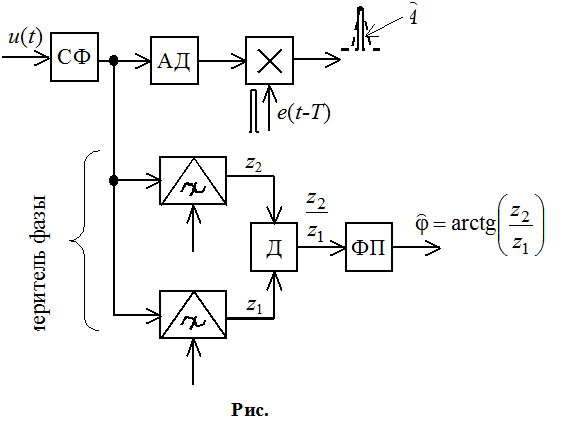
Необходимо вычислить интеграл и искать a, при котором она максимальна. Этот метод реализуется с помощью многоканальной схемы:

При любом a, максимум по j будет получаться при:

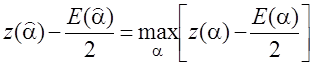
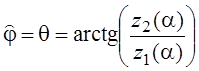  - для энергетических параметров

Для неэнергетических параметров:

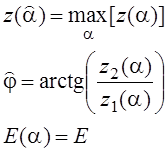
Можно использовать ту же многоканальную схему. Получим тот же результат, если учесть, что I₀(x)=e^x .

2.3 Оценка энергетических параметров. Оценка амплитуды сигнала

Мы считаем, что неизвестна А . s(t₁,A)=As₁(t), где s₁(t) - определяет форму сигнала.

u(t)=A s₁(t)+n(t)

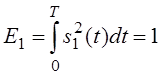
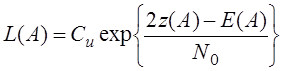
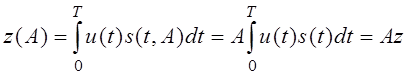
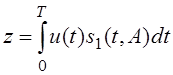
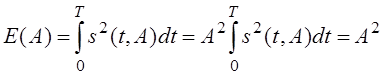- энергия сигнала

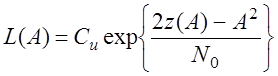
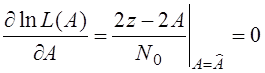
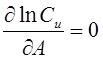
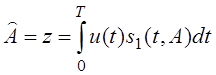- оценка выходной величины коррелятора

    Нам необходимо включить каскад, который будет опрашивать в момент t=T :

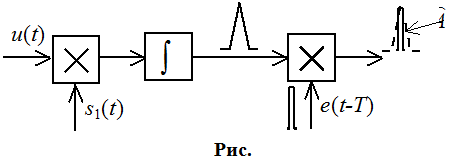
Для согласованного фильтра:

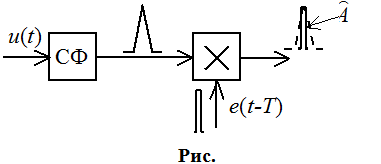
Найдём матожидание  и дисперсию  :

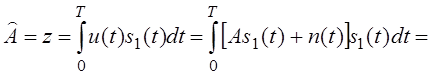
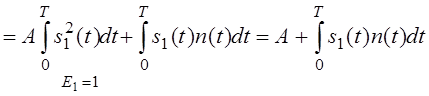 - оценка и шумовая добавка.

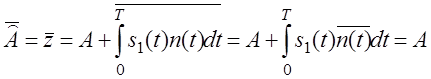 ,так как 

так как  , то оценка несмещенная. Дисперсия равна:

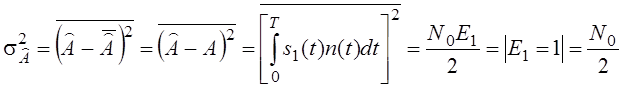
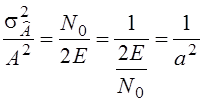        - относительная погрешность.

При измерении начальной фазы :

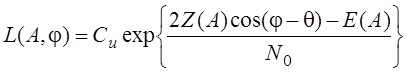
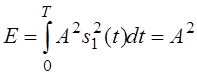
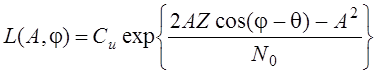
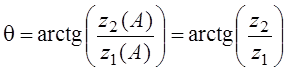
Пусть известны А и :

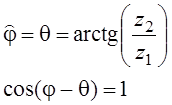
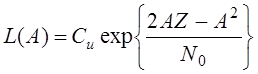
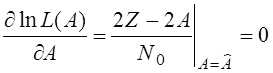
- огибающая корреляционного интеграла.