Особенности работы при недостаточной информции помеховой обстановке

Лекция 33. Особенности работы при недостаточной информции помеховой обстановке

Эффективность ранее рассмотренных методов обработки сигналов при различных формах избыточности определялась точностью оценки параметров помеховой обстановки, необходимых для функционирования того или иного алгоритма. При этом применение классических методов оценки, известных из статистической теории связи, осложняется в практической обстановке.

Современные реальные условия работы систем связи, как правило, всегда характеризуются значительной априорной неопределенностью (АН) обстановки. При этом  информации обычно недостаточно не только о необходимых значениях параметров, но иногда и о видах помех и о структуре помеховой обстановки, особенно в условиях радиопротиводействия.

Так как в практических условиях виды возможной помеховой обстановки обладают исключительным разнообразием, то и состав априорной информации о ней также может варьироваться в широких пределах. Поэтому классические статистические алгоритмы могут дополняться особенностями, с различных позиций учитывающими априорную неопределенность обстановки.

Большое значение имеет объем и форма описания совокупности исходных априорных сведений об обстановке в районе расположения станции связи. Как известно, наиболее полно взаимосвязь между требуемыми характеристиками описывают соответствующие многомерные функции распределения. В случае априорной определенности (АО) вид функций известен. В случае АН о них имеются лишь ограниченные сведения.

Любую функцию распределения можно охарактеризовать определенной совокупностью параметров, например, моментами распределения, кумулянтами и др. Для этой цели могут использоваться также специально сконструированные параметры. Обозначим их совокупность в виде вектора  (в общем случае бесконечномерного), определяемого в бесконечномерном Гильбертовом пространстве.

Совокупность априорных сведений о параметрах помеховой обстановки (ППО) может быть представлена в виде:

- набора границ областей определения взаимно-независимых элементов этого вектора ;

- зависимости между этими элементами в виде набора некоторых            функций;

-  в виде функционалов;

-  в форме комбинаций этих видов.

В общем случае их можно свести к первому виду, вводя дополнительны параметры, сконструированные тем или иным способом. Однако в некоторых случаях может оказаться проще использовать их по отдельности. В общем случае совокупность сведений образует некоторый гиперообъем  определенной формы в многомерном пространстве параметров. Размеры объема  характеризуют уровень априорной неопределенности. В случае априорной определенности (АО), объем  стягивается в точку, в случае полного отсутствия исходных сведений  занимает все многомерное пространство.

Реальная ситуация неполного объема исходных сведений представляет собой промежуточный случай, когда размеры объема  в соответственно выбранной мере - некоторая конечная величина (несмотря на то, что  - бесконечномерный.). Когда форма взаимосвязи между какими-либо вероятностными параметрами ППО - тоже вероятностная, совокупность  всегда можно переформировать таким образом (например, добавлением новых измерений, либо новых функциональных связей между элементами), чтобы выразить набор априорных сведений о параметрах в виде объема .

Известно, что если реализация векторного сигнала , как случайного процесса, представлена в виде совокупности некоррелированных отчетов, то при этом достаточная статистика многомерной случайной величины Z, зависящей от параметра , которая требуется для оценки этого параметра - это функция правдоподоподобия L(q)=W(Z/q).

В случае полностью известных параметров построение оптимальных процедур оценки с использованием  направлено на минимизацию потерь, обусловленных статистическим характером оцениваемых величин. В случае АН добавляется вторая составляющая потерь, обусловленная неполной информацией о значениях параметров , описывающих распределение W(Z/q)=W(Z/q,l). Оптимизация процедуры оценки при этом должна производиться с целью уменьшения общих потерь от неточности оценивания.

Для оценки ППО, требуемых для работы алгоритмов подавления помех, используем комплексный критерий, представляющий собой модификацию известного минимаксного критерия.  Он основывается на следующем.  Потери от неточности оценивания пропорциональны мощности остаточной после компенсации части внешней помехи. Функция потерь  от использования оценки параметра  вместо его значения , будет представлена, как квадратичная форма от погрешностей измерения составляющих вектора весовых коэффициентов. Последующие рассуждения, приводимые для одного параметра , могут быть обобщены на случай нескольких параметров.

При полностью известных параметрах байесов критерий предполагает минимизацию среднего риска.

.

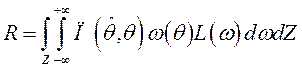Распределение , оцениваемого параметра  считается равномерным внутри его области значений (если нет объективных причин отдавать предпочтение каким-либо его отдельным значениям). Оптимальная оценка  соответствует минимальному среднему риску R_o.

Учет влияния АН ППО будет производиться следующим образом: Как известно, потери из-за неправильного оценивания при использовании оценки  вместо истинного значения параметра  (обусловленные статистическим характером оценки) равны среднему риску R. Теперь рассмотрим другую ситуацию, когда при известном истинном значении параметра  в алгоритмах обработки сигналов тем не менее используется некоторое другое значение, равное  . Это тоже будет сопровождаться определенными потерями. Если приравнять потери от использования неточного значения параметра , имеющие место в обеих ситуациях, то погрешности оценивания также может характеризовать отличием величины  от величины . В результате подобного величина  определяется уравнением