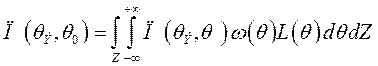Особенности работы при недостаточной информции помеховой обстановке, страница 2

.

Решение этого уравнения всегда дает два значения для  и , поскольку функция  имеет две ветви. Если функция симметрична относительно , то 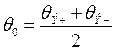. Когда объем выборки Z бесконечно большой (в условиях полностью известных параметров), , ошибка при оценивании равна нулю. При конечном объеме выборки, минимум среднего риска R соответствует минимуму разности . Таким образом, использование характеристик  и , так же, как среднего риска R, позволяет учитывать и минимизировать статистическую погрешность оценивания, но при этом одновременно дает возможность учета и влияния априорной неопределенности.

Влияние АН на характеристики  и  выражается в следующем. В условиях АН функция правдоподобия  зависит от совокупности параметров , и при перемещении вектора  внутри объема априорной информации  вид  будет меняться, соответственно меняться и величина среднего риска. При этом  и  перемещаются внутри некоторых областей  и .

Объем  получен из набора априорных сведений, все значения внутри его равноправны. Здесь необходимо особо оговорить, что представление распределения  внутри  равномерным (например, с целью последующего усреднения) неприемлемо, так как тем самым искусственно вносятся дополнительные условия на форму функции , хотя основания для этого в наборе исходных сведений о помеховой обстановке отсутствуют. Из равноправия всех значений внутри объема L₀ не следует их равномерного распределения внутри его. Поэтому для оценки необходимо использовать те значения  внутри , которые соответствуют граничным случаям, либо предпринимать дополнительные меры по получению информации о помеховой обстановке, и, тем самым, для уменьшения объема . Все значения внутри интервала (, ) также равноправны.

В связи с этим критерием качества оценивания, учитывающим одновременно статистический характер величины и неполные априорные сведения о функции правдоподобия (о помеховой обстановке) может служить некоторая величина ε, пропорциональная общей ошибке оценивания (и отражающая потери из-за этой ошибки). Она определится, как разность между точными верхней и нижней гранями множеств  и , которые можно определить, как максимум и минимум по соответствующим областям

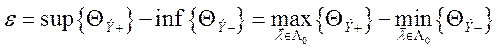                 (1)       

Наилучшей будет оценка , соответствующая минимальным потерям ε₀ по (1). Используемый критерий входит в класс минимаксных критериев, однако использование именно его в предлагаемой форме позволяет получить удобные в практическом применении  квазиоптимальные критерии оценивания в условиях АН. В случае оценки нескольких параметров, все рассуждения без существенных изменений относятся к представлению , как многомерной величины. В этом случае оптимальная оценка  минимизирует ε по каждой из составляющих .

На основе приведенных рассуждений можно заключить,что функционирование систем связи может иметь место в разнообразных условиях помеховой обстановки. Поскольку необходимые ППО, как правило, точно не известны или их определение сопряжено с большими трудностями, то оценка требуемых для подавления помех параметров  производится в условиях априорной неопределенности.

Использование предложенного критерия, учитывающего общие потери, позволяет применить в условиях АН известный метод моментов при оценке параметров, необходимых для алгоритмов компенсации. В условиях априорной определенности предпосылки использования метода моментов заключается в том, что при большом объеме выборки Z измеряемые выборочные моменты  с большой точностью совпадают с истинными моментами  функции распределения , где q - неизвестный параметр, который требуется оценить.

При этом, в совокупности параметров l, известных заранее, заключена тем или иным способом информация о виде функции распределения W. Поскольку вид функции W и значения параметров l известны, то известны и функциональные зависимости, определяющие параметры  через l и . Эти зависимости могут задаваться системой уравнений

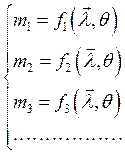                                                                                 (2)

С использованием этих формул можно получить выражения, определяющие  через  и . B зависимости от того, какие именно параметры будут использоваться сформировать совокупность различающихся между собой уравнений, в общем случае, любого объема