Особенности работы при недостаточной информции помеховой обстановке, страница 4

Она может стать настолько значительной, что сделает невозможным последующее использование алгоритмов компенсации. Таким образом, в подобной ситуации состояние канала связи не позволяет непосредственно использовать метод моментов для оценки требуемых параметров. В то же время приложение метода моментов в видоизмененной форме и в этой ситуации даст возможность определять нужные параметры с требуемой точностью. Покажем путь его применения.

Составим систему уравнений, взяв два из тех, что связывают следующие начальные и центральные моменты:

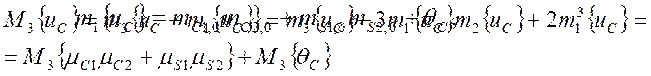Отсюда требуемый параметр, определяемый по каждому из этих уравнений, необходимо вычислять по формулам:

Из априорных данных следует, что распределения m_С1, m_С2, m_S1, m_S2- гауссовы, следовательно, они симметричные относительно их среднего значения. Если процессы  m_C1, m_S1 симметричны и независимы, то их произведение также симметрично. То же относится к процессам  и. Независимость обусловлена пространственным разнесением. Сумма симметричных процессов тоже симметрична независимо от их взаимозависимости.

Таким образом, распределение величины m_C1m_C2+m_S1m_S2 симметрично относительно среднего при произвольных значениях параметров распределений этих процессов. При этом третий центральный момент этого выражения всегда равен нулю. Поэтому, если множество   имеет некоторые ненулевые линейные размеры.

Результирующее множество  также, представляет собой точку, следовательно, использовать зависимости величины q_С от других моментов распределений нет необходимости. Также, одновременный учет оценки q_С,  не ведет к дополнительному увеличению точности.  После аналогичных рассуждений несложно получить также оценку параметра .

Обозначим искомый фазовый сдвиг между помеховыми компонентами через y₀. Тогда параметры  будут равны, соответственно

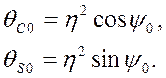Таким, образом, оценки амплитудно-фазовых соотношений помеховых компонент при двукратном разнесении, полученные модификацией метода моментов для условий АН, приобретают вид

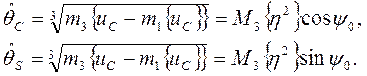Этот факт обусловлен тем, что третий центральный момент от распределения комбинации полезных сигналов равен нулю в связи с его симметричностью. А третий центральный момент от распределения квадрата величины  будет равен нулю лишь при специальном выборе вида этого распределения. (Это является ограничением метода). Величина  в общем случае неизвестна, но это не имеет значения, т.к. для компенсации необходимо знать величину угла , определяемого отношением параметров   и  .

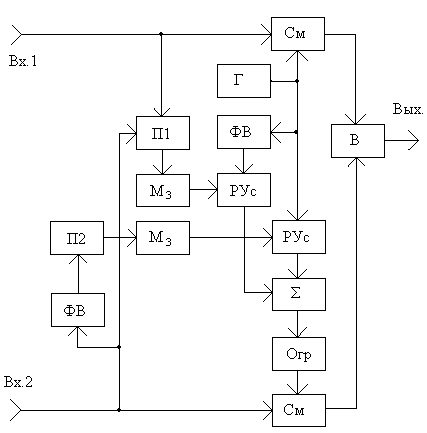
Пример реализации подобной обработки приведен на укрупненной структурной схеме, рис. 33.1. В перемножителях (П1 и П2) производится определение величин  и . Соответствующие ортогональные компоненты получаются после прохождения фазовращателей (ФВ) на 90⁰. В блоках М₃ производится вычисление величин   и  . В генераторе (Г) вырабатывается некоторое вспомогательное синусоидальное напряжение. Из него формируются два ортогональных напряжения, подаваемые на регулируемые усилители (Рус). Их коэффициенты передачи пропорциональны выходным сигналам блоков М₃. Далее они складываются в сумматоре S и подвергаются амплитудному ограничению в ограничителе (Огр). Уровень ограничения таков, что амплитуда сигнала после ограничителя становится равна амплитуде выходного сигнала генератора.

Таким образом, на смесители (См) подаются два сигнала с разностью фаз, равной . На другие входы смесителей поступают два входных разнесенных сигнала, помеховые компоненты в которых различаются по фазе также на . Фильтры смесителей выделяют разностную частоту, в результате этого на их выходах помеховые компоненты оказываются синфазными. Поэтому после взаимного вычитания в блоке вычитания (В) полезные сигналы освобождаются от помеховых составляющих. Устройство, реализующее описанный выше принцип оценки параметров, укрупненная структурная схема которого соответствует приводимой на рис. 33.1. В случае, если вид распределения помехи известен лучше, для оценки может быть использована сумма нескольких нечетных центральных мо

ментов величин  и , так как все нечетные центральные моменты суммы m_C1m_C2 + m_S1m_S2 равны нулю