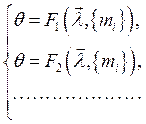Особенности работы при недостаточной информции помеховой обстановке, страница 3

                                                                          (3)

Все уравнения равноправны, подстановкой в любое из них выборочных параметров  вместо , получаем . При практическом использовании из совокупности уравнений (2) выбирается, как правило уравнение, имеющее наиболее простой вид.

Ситуация значительно меняется в условиях априорной неопределенности. Вектор  может находиться в любой точке объема . При этом посредством каждого из уравнений (2) множество точек объема  отображается в отдельные множества

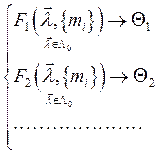                                                        (4)

Эти множества, как правило, не совпадают. В то же время истинное значение  принадлежит одновременно всем  и лежит внутри некоторого множества , представляющего собой их общую часть                                     

Очевидно, что ошибка оценки  равна

и с ростом числа используемых уравнений уменьшается или, по крайней мере, не возрастает. Как ранее получено, оптимальной будет оценка, лежащая в «середине» общего множества, определяемого на основе этой формулы, т.е.

.

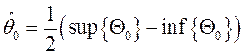Если последовательно учитывать эти уравнения, то с каждым новым уравнением границы (одна или обе) будут сужаться (или по крайней мере не расширяться). Поэтому из всех возможных уравнений при формировании  должны участвовать те из уравнений системы, которые при подстановке в них параметров  дают максимальное сужение границ . Вопрос об их общем количестве решается в каждом конкретном случае отдельно.

На основе изложенного общего подхода рассмотрим в качестве одного из примеров применения метода синтез устройства компенсации помех для случая двукратного разнесения (N=2) и воздействия одиночной помехи (М=1). Поскольку разнесенные приемные антенны обычно достаточно идентичны по свойствам и одинаково ориентированы, то помеховые составляющие во входных сигналах близки по уровню и отличаются один от другого лишь относительным фазовым сдвигом.   Сигналы в двух разнесенных приемниках в этом случае могут быть описаны, как

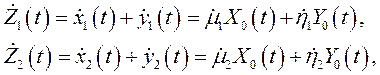
где  - нормированный по мощности помеховой сигнал, .

Будем считать, что помеховые составляющие обеих ветвей значительны по уровню, (кроме того модули @=h). Аргументопределяется коэффициентами передачи по каналу «источник помехи – приемник» и при неподвижном или медленно перемещающемся источнике помехи может рассматриваться по сравнению с величинами , как величина постоянная или изменяющаяся значительно медленнее. Для осуществления компенсации необходимо узнать этот фазовый сдвиг, который однозначно определяется соотношением величин 

Знак тильды «~» обозначает величину, сопряженную по Гильберту с исходной.

Пусть m_С1, m_S1, m_C2, m_S2 - ортогональные составляющие комплексных элементов , - вектора . Тогда напряжения

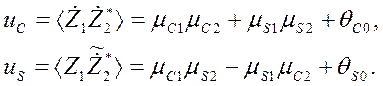Распределение компонент m_C1, m_C2, m_S1, m_S2 – гауссово. Если распределение амплитуд вектора  - рэлеевское, то математические ожидания этих четырех компонент равны нулю. Однако в реальных условиях большой процент времени вид распределения быстрых замираний отличается от рэлеевского, в частности параметры m_C1, m_S1, m_C2, m_S2 могут иметь постоянную составляющую. Поскольку функция потерь, зависящая от двух аргументов q_C и q_S, представляет собой величину, пропорциональную сумме квадратов отклонений их оценок от истинных значений параметров q_C0, q_S0, то вклады в общие потери от неточности их оценок взаимно независимы, и определение оптимального вида оценок параметров q_C и q_S можно производить по отдельности и также независимо.

Рассмотрим параметр q_C.

Ошибку из-за наличия постоянных составляющих нельзя устранить усреднением, поскольку значения этих постоянных составляющих неизвестны и они относятся к группе априорно неизвестных параметров в совокупности . Величина этой ошибки равна