Особенности работы при недостаточной информции помеховой обстановке, страница 5

.

Рис. 33.1.

Работа алгоритма определения требуемых параметров моделировалась с использованием ЭВМ. Некоторые результаты моделирования процесса настройки приведены на рис. 33.2 – 33.4.

Распределение помехового компонента моделировалось гауссовым (рис. а)) и равномерным (рис. б)) законами. Значения параметров задавалось в относительных единицах. Средняя мощность помеховой составляющей обеих ветвей была равна 0,5. Параметры четырехпараметрического распределения полезных сигналов задавались следующими.

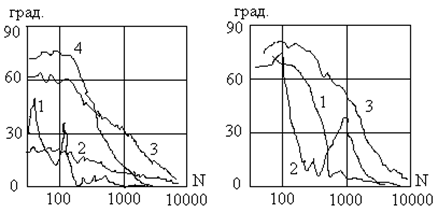Рис. 33.2,а)               Рис. 33.2,б)

Рис.33.3,а)                           Рис.33.3,б)

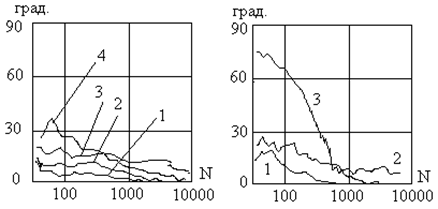Рис. 33.4,а)                    Рис.33.4, б)

На рис. 33.2 имитировалось рэлеевское распределение амплитуд полезных сигналов, при этом средние значения регулярных составляющих ортогональных компонентов коэффициента передачи для всех графиков   среднеквадратическое отклонение - графики под номером:

1 -    ;

2 -    ;

3 -     ;

4 -    .

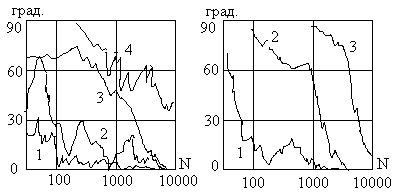
На рис. 33.3 исследовались случаи, когда среднеквадратичные отклонения различных компонентов неодинаковые (средние значения равны нулю, как и в предыдущих графиках). Графики 1 построены для параметров

1 -    , ;

2 -    ,;

3 -    , ;

4 -     , .

Графики на рис. 33.4 а). соответствуют обобщенно-рэлеевскому распределению. На всех графиках . Другие параметры:

График 1.  

График 2.  

График 3.  

График 4.  

Графики на рис.33.4 б). соответствуют неравным среднеквадратическим отклонениям в ветвях. На всех графиках  Другие параметры:

График 1.  

График 2.  

График 3.  

По оси ординат отложена в градусах разница между истинным углом между помеховыми составляющими и его оценкой, т.е.ошибка оценивания. По оси абсцисс отложена длина выборки, использованная для оценивания.

Непрерывные процессы изменения уровня входных сигналов заменялись их отсчетами. Отсчеты полагались независимыми. Этот факт позволяет «безразмерное» время, использованное при моделировании, соотнести с реальным временем, приравнивая безразмерный дискрет по оси времени приведенных графиков к интервалу времени между соседними значениями уровня сигнала на реальных трассах, которые могут считаться независимыми. Таким образом, могут быть определены границы применимости метода в конкретных условиях.

Из графиков можно сделать вывод, что время подстройки сильно зависит от соотношения мощностей полезных и помеховых компонентов. Если мощность помехи меньше, чем мощность полезного сигнала, то процесс подстройки достаточно длителен. Если мощность помехи выше мощности полезного сигнала, то процесс подстройки завершается достаточно быстро. Скорость подстройки заметно зависит и от вида распределения помехи. Неравенство параметров четырехпараметрического закона распределения полезных компонентов, относимых к разным осям координат, не оказывает определяющего воздействия на скорость подстройки.

Большая глубина замираний амплитуды полезного сигнала при малой регулярной составляющей и, наоборот, большая регулярная составляющая при малой глубине замираний соответствуют достаточно большой скорости подстройки. В то же время, когда и регулярная составляющая, и глубина замираний достигают заметного уровня, скорость подстройки значительно снижается.

Приведенные рассуждения предполагали стационарность случайных процессов колебания величины ортогональных компонентов сигналов, а также постоянства по времени амплитудно-фазовых различий помеховых составляющих в ветвях разнесения. Это предполагает, что источник помех неподвижен. На реальных трассах случайный процесс изменения уровня сигналов – это нестационарный процесс, т.е.  изменение параметров быстрых замираний определяется скоростью медленных замираний.

Графики позволяют определить, сколько времени в различных условиях займет определение с необходимой точностью параметров для подавления помех. Подавление помех будет в этих условиях эффективным только в том случае, если изменение параметров за счет медленных замираний в течение этого времени не превысит точности измерения.