Лекция 16. Цифровые виды модуляции. Дискретизация и квантование сигналов
Замена аналогового сигнала S(t) импульсной последовательностью, состоящей из отсчётов аналогового сигнала в определенные моменты времени Si(tk), называется дискретизацией сигнала. Передача дискретной информации позволяет использовать аппаратуру для одновременной передачи информации от ряда различных источников в моменты времени, смещенные относительно отсчётов первого информационного сигнала. Этот процесс назвали временным уплотнением каналов передачи информации, и он исключительно широко используется на практике. Другое важнейшее свойство дискретной формы представления и передачи информации заключается в возможности восстанавливать искаженный импульсный сигнал (регенерировать не искаженный по форме импульс).
При дискретизации, называемой также импульсным преобразованием непрерывного сигнала, возникают две принципиально важные задачи:
- как выбирать интервал дискретизации, т. е. временной интервал между отсчетами;
- какова погрешность от замены непрерывного сигнала импульсной последовательностью.
Сформулированная в 1928 году английским ученым Найквистом, доказанная в 1931 году В.А. Котельниковым и примененная им к практическим задачам передачи информации в 1933 году теорема о минимальном числе отсчётов при дискретизации аналогового сигнала во времени, обосновала возможность заменять аналоговые сигналы их импульсными отсчётами, следующими друг за другом через временные интервалы Ti. В 1948 году американский ученый Клод Шеннон назвал эту теорему теоремой отсчетов, но в нашей стране она справедливо именуется теоремой Котельникова.
При частоте следования импульсных отсчётов не менее чем удвоенной верхней частоты спектра дискретизируемого сигнала
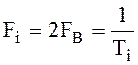 аналоговый сигнал восстанавливается путем пропускания
потока отсчётов через фильтр нижних частот с частотой среза 1/2Ti и аналоговая функция определяется полностью и однозначно.
аналоговый сигнал восстанавливается путем пропускания
потока отсчётов через фильтр нижних частот с частотой среза 1/2Ti и аналоговая функция определяется полностью и однозначно.
В.И. Котельников, применив теорему отсчётов к задачам связи, показал, что любой аналоговый сигнал S(t) можно представить рядом вида:
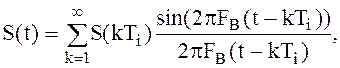 (1)
(1)
где ![]() – период дискретизации.
– период дискретизации.
Выражение (1), называемое
рядом Котельникова, даёт ответ на обе задачи: как выбрать интервал дискретизации
![]() и как точнее восстановить функцию S(t).
и как точнее восстановить функцию S(t).
Ряд имеет два сомножителя у
каждого члена - это S(kTi) и  . Сомножитель
. Сомножитель  представляет собой импульсную характеристику идеального
ФНЧ с частотой среза FB,
т.е. его реакцию на воздействие импульсной функции Дирака (очень короткого
представляет собой импульсную характеристику идеального
ФНЧ с частотой среза FB,
т.е. его реакцию на воздействие импульсной функции Дирака (очень короткого ![]() -импульса).
-импульса).
Каждый член ряда Котельникова можно рассматривать как отклик ФНЧ на короткий импульс, площадь которого пропорциональна S(kТi). Если на вход такого фильтра подать регулярную последовательность отсчетов Si(tk) в виде коротких импульсов, например прямоугольных, с амплитудой пропорциональной Si(tk), то на выходе ФНЧ суперпозиция откликов образует [1] непрерывную функцию времени, повторяющую в масштабе исходный аналоговый сигнал S(t), показанный на рис.16.1.
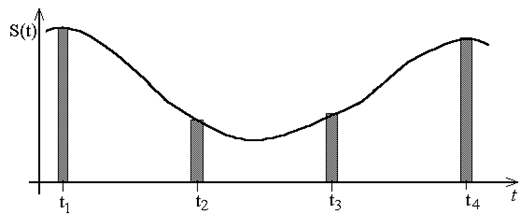 |
Рис. 16.1. Дискретизация аналогового сигнала
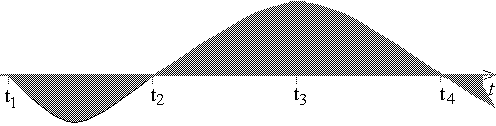 |
 , показанный на рис. 16.2. На выходе ФНЧ
получим сумму всех откликов, равную S(t), показанную на рис. 16.3.
, показанный на рис. 16.2. На выходе ФНЧ
получим сумму всех откликов, равную S(t), показанную на рис. 16.3.
Рис. 16.2. Пример отклика ФНЧ на одиночный импульс
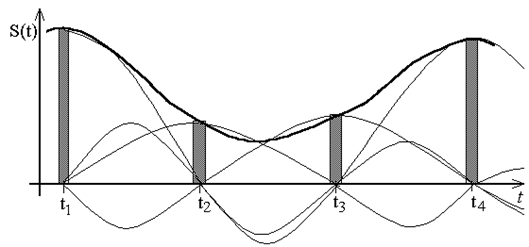 |
Рис. 16.3. Восстановление аналогового сигнала суммой откликов ФНЧ
Частота FB выбирается так, чтобы энергия сигнала ![]() , находящегося в спектре выше частоты FB, была много меньше полной энергии сигнала Е. Тогда сигнал
длительностью t определяется конечным числом отсчетов
(целой частью рассчитанного значения), называемым также базой сигнала В:
, находящегося в спектре выше частоты FB, была много меньше полной энергии сигнала Е. Тогда сигнал
длительностью t определяется конечным числом отсчетов
(целой частью рассчитанного значения), называемым также базой сигнала В:
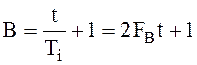 , и может быть интерполирован рядом
Котельникова со
среднеквадратической ошибкой интерполяции в пределах [1]:
, и может быть интерполирован рядом
Котельникова со
среднеквадратической ошибкой интерполяции в пределах [1]:
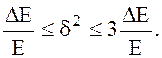
В общем случае для
воспроизведения сигнала длительностью t при
полосе частот FН - FB необходимо передавать по линии число
параметров не менее ![]() , где ΔF= FB - FН.
, где ΔF= FB - FН.
Отметим, что при малых частотах дискретизации растёт ошибка δ2 из-за роста ΔЕ. Обычно частоту дискретизации выбирают на 10 – 20 % выше 2FВ, что обеспечивает высокую точность воспроизведения сигнала S(t) и не вносит большую избыточность в дискретизирующую импульсную последовательность.
Дискретизация может быть равномерной во времени с постоянным интервалом дискретизации и неравномерной, когда положение отсчётов на временной оси зависит от характеристик дискретизируемого сигнала. Наиболее проста в реализации равномерная дискретизация, и именно она получила широкое применение на практике.
Амплитудно-импульсная модуляция
Различают амплитудно-импульсную модуляцию двух видов - АИМ-1 и АИМ-2. Фактически эти подвиды различаются формой дискретизирующих аналоговый сигнал импульсов. При АИМ-1 огибающая дискретизирующих импульсов повторяет форму огибающей аналогового сигнала, а при АИМ-2 дискретизацию осуществляют прямоугольными импульсами, как показано на рис. 16.4.
Более качественный вид модуляции АИМ-1, так как в этом случае минимальны частотные искажения спектра и минимальна ошибка. При гармонической модуляции прямоугольных импульсов в спектре АИМ-1 содержится несущее колебание, два боковых и два симметричных колебания с равной амплитудой около каждой гармоники частоты дискретизации.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.