Структура построения и параметры РРЛ. Общие сведения, страница 18

7.  По формуле (6.14) или по номограмме рисунку 6. по известным параметрам   находим величину, характеризующую радиус кривизны препятствия:

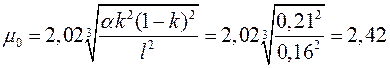
8.  По формуле (6.17) определяем . Предварительно по формуле (6.18) находим параметр d:

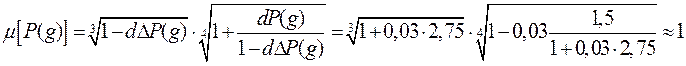
Таким образом, .

Из примера видно, что даже в области глубокой тени в дальнейших расчетах будем считать  

9.  Из рисунка 7 при  = 2,42 находим V₀ = −8,3 дБ.

10.  По формуле (6.43) (см выше) и учитывая, что  определяем величину множителя ослабления для закрытой трассы:

Поскольку , то для определения V можно было также воспользоваться графиком рисунок 6, с помощью которого при  находим V = −21 дБ.

11.  Для построения графика зависимости V= f(g) необходимо получить еще несколько точек, задаваясь другими значениями gдля области, где                  P(g)< l, т.е. для H(g) < H₀(для полузакрытых и закрытых трасс), например, g= + 1010^-8 1/м и g= 0. Результаты расчетов приведены в табл. 8.

Таблица 8. Результаты расчета множителя ослабления

g10-8, м-1	+25	+10	0	−5	−14	−18	−22,5
P(g)	−1,5	-0,26	+0,575	+1	+1,73	+1,9	+2,45
V, дБ	−21	−10,4	−3,5	0	+1,4	+0,76	−2

12.  По интерференционной формуле ((6.11) из [1]) определим множитель ослабления в освещенной области (зона интерференции), где p(g) >1 и наблюдается интерференционная картина поля.

          (6.44)

Относительный просвет, при котором наблюдаются интерференционные максимумы поля в месте расположения приемной антенны, найдем по формуле:

Для первого интерференционного максимума, т. е. при m= 1.

13.  Зная величину относительного просвета и используя формулу (6.10), не трудно найти просвет, соответствующий этому максимуму:

14.  Приращение просвета, при котором достигается ,

15.  По формуле (6.3) или по номограмме рисунок 5 определим

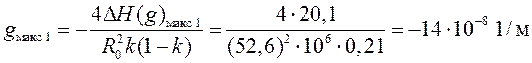
16.  Для определения множителя ослабления по той же интерференционной формуле (6.44) необходимо знать коэффициент отражения от земной поверхности для отраженной волны, создающей первый интерференционный максимум. Из профиля трассы, представленного на рисунке 15, известно, что подстилающая поверхность в точке отражения (наивысшая точка профиля) покрыта лесом и имеет выпуклую поверхность. Поэтому на основании формулы ((6.22) из [1]) Ф=1D. По формуле ((6.23) из [1]) находим

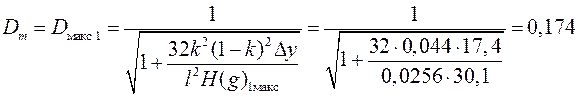
17.  Множитель ослабления в первом интерференционном максимуме определяется по формуле ((6.19) из [1]):

18.  Относительный просвет, при котором возможны минимумы поля, определяются по формуле ((6.16) из [1]):

 При n = 1

19.  По формуле (6.10) найдем величину просвета, соответствующую первому интерференционному минимуму:

20.  Первый интерференционный минимум возможен при изменении величины просвета на величину

21.  По формуле (6.3) или по номограмме рисунок 5 определяем градиент , при котором  возможно попадание в первый интерференционный  минимум:

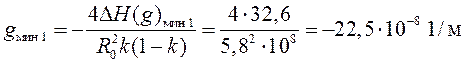
22.  Для определения множителя ослабления V в первом интерференционном минимуме по формуле ((6.17) из [1]), необходимо по формуле ((6.25) из [1]) рассчитать значение коэффициента отражения в этом минимуме :

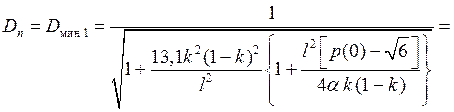
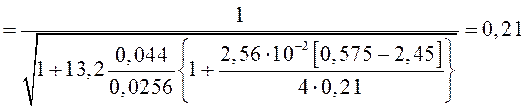
Иногда при расчетах величина D_n получается больше единицы, это значит, что профиль трассы становится вогнутым. В этом случае при расчетах V вблизи минимума следует считать

23.  По формуле ((6.17) из [1]) находим

24.  Задаваясь различными значениями g (например, g = −510⁻⁸ ,−1010⁻⁸, −1610⁻⁸ 1/м и т. д.) и подставляя их в интерференционную формулу, получим ряд промежуточных значений V.

25.  Пусть g= −510⁻⁸ 1/м. По формуле (6.3) или по номограмме рисунок 5 определяем изменение просвета

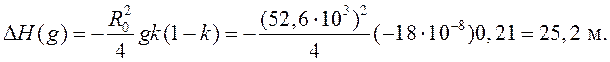
26.  Значение просвета на трассе с учетом рефракции

27.  Относительная величина просвета