Федеральное агентство по образованию Российской Федерации
Государственное образовательное учреждение
высшего профессионального образования
Владимирский государственный университет
Кафедра конструирования и технологии радиоэлектронных средств
лабораторная работа 2
«оценка генеральных характеристик параметра качества по выборочным значениям»
по дисциплине: «Математические основы проектирования электронных средств»
Выполнил:
студент гр. Р-105
Руководитель:
Владимир 2007
1 Цель работы: изучение методов оценки генеральных характеристик по выборочным значениям.
2 Тип элемента и его номинальное значение
В качестве однотипных радиоэлементов использовались резисторы с номинальным сопротивлением 1 кОм, в качестве измерительного прибора использовался мультиметр.
3 Измеренные значения параметров элементов
Таблица 1 Измеренные величины сопротивлений.
|
№ |
1-ая выборка R,Oм |
2-ая выборка R,Oм |
|
1 |
992 |
988 |
|
2 |
1008 |
1003 |
|
3 |
1012 |
1009 |
|
4 |
1001 |
991 |
|
5 |
998 |
998 |
|
6 |
998 |
988 |
|
7 |
1007 |
987 |
|
8 |
992 |
1005 |
|
9 |
995 |
972 |
|
10 |
988 |
999 |
|
11 |
992 |
1007 |
|
12 |
999 |
994 |
|
13 |
988 |
995 |
|
14 |
990 |
988 |
|
15 |
999 |
991 |
|
16 |
994 |
1000 |
|
17 |
990 |
991 |
|
18 |
997 |
1000 |
|
19 |
1006 |
979 |
|
20 |
993 |
1025 |
Необходимо определить доверительные интервалы для математического ожидания и дисперсии при объемах выборок n = 10; 15; 20 и при различных доверительных вероятностях γ = 0,8; 0,9; 0,95. Всего производится две выборки.
Доверительный
интервал для математического ожидания ![]() находится по неравенству:
находится по неравенству: 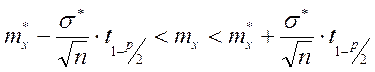 , где
, где ![]() - среднее арифметическое,
находится по формуле:
- среднее арифметическое,
находится по формуле: 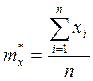 ;
;
![]() - стандарт
сопротивления в выборке, определяется:
- стандарт
сопротивления в выборке, определяется:
![]() ,
, ![]() -
выборочная дисперсия:
-
выборочная дисперсия:
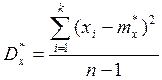 ;
;
![]() — объем выборки;
— объем выборки;
![]() — уровень значимости;
— уровень значимости;
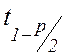 — квантиль распределения Стьюдента,
определяемый по уровню значимости
— квантиль распределения Стьюдента,
определяемый по уровню значимости ![]() и
числу степеней свободы f = n – 1.
и
числу степеней свободы f = n – 1.
Доверительный интервал для дисперсии при
нормальном законе распределения равен:
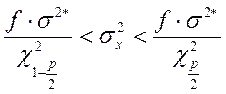 , где
, где ![]() —
выборочная дисперсия;
—
выборочная дисперсия;
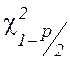 ,
, ![]() —
квантили распределения Пирсона, определяемые из таблицы по уровню
значимости
—
квантили распределения Пирсона, определяемые из таблицы по уровню
значимости ![]() и числу степеней свободы
и числу степеней свободы ![]() .
.
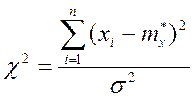
Для 1-ой выборки, состоящей из 10 элементов и доверительной вероятности γ = 0,8 определяются доверительные интервалы для математического ожидания и дисперсии:
т.к. γ + р = 1, уровень значимости р = 1-0,8 = 0,2. Число степеней свободы f =10– 1 = 9.
По таблице находим
квантиль распределения Стьюдента 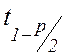 = 1,38.
= 1,38.
Тогда среднее арифметическое:
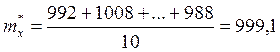 Ом.
Ом.
Выборочная дисперсия:
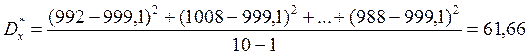 Ом2, а стандарт сопротивления равен:
Ом2, а стандарт сопротивления равен: ![]() Ом
Ом
Тогда доверительный интервал для математического ожидания:
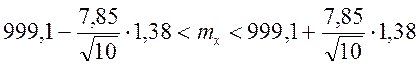 ,
,
![]() .
.
Число степеней свободы ![]() , р = 0,2. По таблице
определяем квантили распределения Пирсона:
, р = 0,2. По таблице
определяем квантили распределения Пирсона: 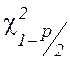 =9,80
,
=9,80
, ![]() =3,82.
=3,82.
Доверительный интервал для дисперсии:
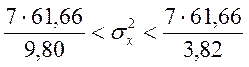 ,
, ![]() .
.
Аналогичные расчеты проводятся для доверительных интервалов при объемах выборок n = 10; 15; 20 и при различных доверительных вероятностях γ = 0,8; 0,9; 0,95. Всего производится две выборки.
В таблице 2 приведены значения квантиля распределения Стьюдента, квантилей распределения Пирсона для заданных значений уровня значимости и числа степеней свободы. В таблице 3 - рассчитанные значения среднего арифметического, выборочной дисперсии. В таблице 4 - рассчитанные значения доверительных интервалов для математического ожидания для двух выборок. В таблице 5 - рассчитанные значения доверительных интервалов для дисперсии для двух выборок.
Таблица 2 Значения квантиля распределения Стьюдента, квантилей распределения Пирсона для заданных значений уровня значимости и числа степеней свободы.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.